Rekursio yleisesti¶

Rekursio ohjelmoinnissa¶

Kun puhutaan rekursiosta ohjelmoinnin yhteydessä, niin yleensä aihe liittyy funktioihin. [1] Rekursiivinen funktio on määritelty itsensä avulla eli se kutsuu itseään.

Toteutetaan edellä esitelty kertoman laskeminen rekursiivisella C++-funktiolla:

unsigned int kertoma(unsigned int n) {
    if ( n == 0 ) {
        return 1;
    } else {
        return n * kertoma(n - 1);
    }
}

joka siis laskee ja palauttaa parametrinsa n kertoman.

Periaatteessa funktion voi kirjoittaa suoraan kertoman rekursiivisen määritelmän pohjalta, mutta hyödyllisempää olisi ymmärtää, miksi funktio toimii ja vieläpä oikein.

Oletetaan, että kertoma-funktiota kutsutaan näin:

int main() {
    cout << kertoma(5) << endl;
}

ja tutkitaan vaihe vaiheelta, kuinka suoritus etenee. Pääohjelman funktiokutsun seurauksena päädytään suorittamaan edellä määritellyn kertoma-funktion runkoa. Tilanne voidaan kuvata seuraavasti:

Kuvassa peitettynä oleva main-laatikko kuvaa sitä, että main-funktion suoritus on kesken, eli vasta kun sen peittävä kertoma-funktio suorittaa return-käskyn, jatkuu main-funktion suoritus siitä kohdasta, jossa kertoma-funktiota kutsuttiin.

Koska n:n arvo on 5, suoritetaan else-haara.

Ennen kuin kertoma kuitenkaan voi palauttaa arvon, sen on laskettava arvo lausekkeelle n * kertoma(n - 1), eli sen oma suoritus jää kesken niin pitkäksi aikaa, että rekursiivinen kutsu kertoma(n - 1) saa laskettua 4:n kertoman.

Itse asiassa suoritus etenee tällä rekursiokierroksella täysin samoin kuin edelliselläkin, paitsi että parametrin n arvo on nyt 4:

Suoritus ajautuu siis jälleen else-haaraan ja rekursio etenee aina vain syvemmälle. Huomaa, kuinka taustalle alkaa kertyä myös keskeneräisiä kertoma-funktion suorituksia.

Näin ohjelma etenee, kunnes lopulta saavutaan tilanteeseen, jossa parametrin n arvo on 0:

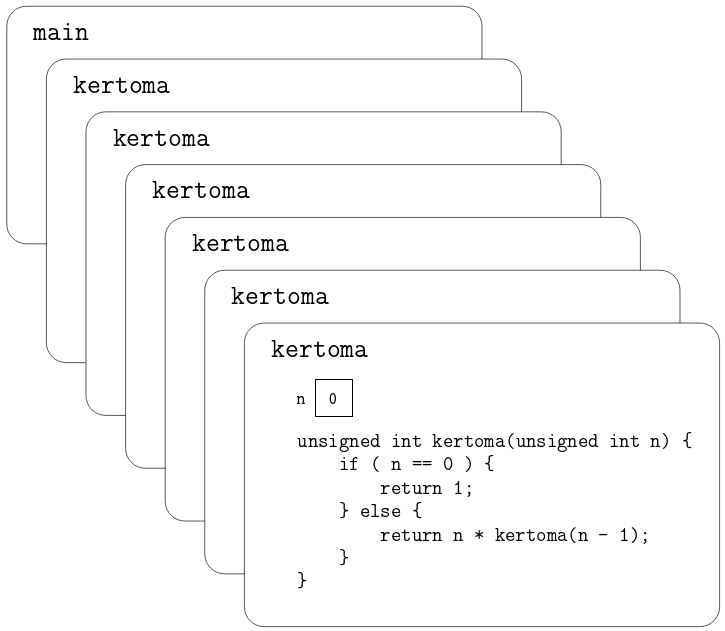
Enää ei tapahdukaan rekursiivista kutsua, vaan kertoma palauttaa suoraan arvon 1 ja keskeneräisten funktiokutsujen pino alkaa purkautua.

Toiseksi viimeiselle kertoma-funktion kutsulle palautuu siis viimeiseltä rekursiiviselta kutsulta arvo 1, joka kerrotaan parametrin n arvolla 1:

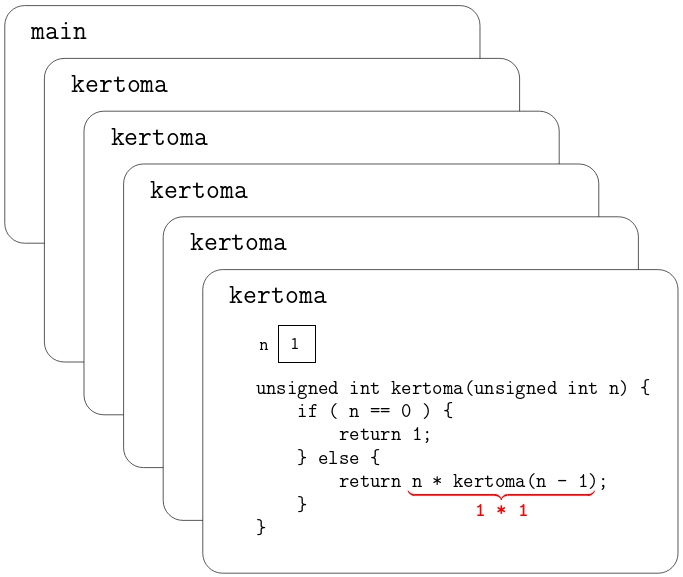
Huomaa että jokaisella kertoma-funktion kutsukerralla (instanssilla) on oma versionsa parametrimuuttujasta n, jonka arvo toki on säilynyt ennallaan, kun rekursiivisesti kutsutusta funktiosta palataan takaisin suorittamaan kutsuneen instanssin käskyjä. Miksi?

Sama pätee kaikkiin paikallisiin muuttujiin.

Seuraavaksi vuorossa oleva keskeneräinen kertoma-funktio jatkuu samaan tapaan:

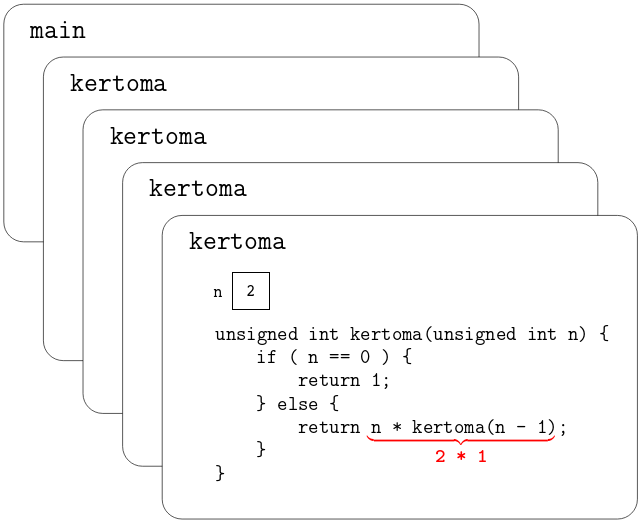
Näin rekursiiviset kutsut purkautuvat ja saavuttavat lopulta ensimmäisen kertoma-funktion instanssin:

Tämä palauttaa pääohjelmalle luvun 5 kertoman arvon:

Rekursiossa ei ole ohjelmointikielen kannalta mitään erikoista: rekursiiviset funktiot ovat funktioita siinä missä kaikki muutkin funktiot. Rekursion vaikeaselkoisuus piilee siinä, että se vaatii ohjelmoijalta ei-luontaista (?) tapaa hahmottaa ongelma ja sen ratkaisu.

Rekursiivisten funktioiden suunnittelua ja ymmärtämistä helpottaa, kun pitää mielessään seuraavat tosiseikat:

• Funktio on rekursiivinen, jos se kutsuu itseään (suoraan tai epäsuoraan).
• Suorituksen kuluessa rekursiivisesta funktiosta on “käynnissä” yhtä monta instanssia, kuin mikä on keskeneräisten rekursiivisten kutsujen lukumäärä.
• Jokaisella instanssilla on omat arvonsa parametreille ja paikallisille muuttujille.

Rekursiivisella funktiolla on kaksi olennaista ominaisuutta, jotka on syytä muistaa:

1. Sillä on oltava lopetusehto (tai ehtoja), joka tunnistaa ongelman triviaalitapaukset ja reagoi niihin ilman uuden rekursiivisen kutsun tarvetta.
2. Jokaisen rekursiivisen kutsun on yksinkertaistettava ratkaistavaa ongelmaa niin, että lopulta päädytään triviaalitapaukseen.

Esimerkin kertoma-funktiossa näitä kohtia edustivat:

1. Ehtolauseen ehto n == 0 on triviaalitapaus: Nollan kertoman arvo tiedetään suoraan.
2. Jokaisella rekursiokierroksella selvitettiin yhtä pienemmän luvun kertomaa: Kutsuparametri pieneni yhdellä.

Jos jommankumman unohtaa, niin funktiota kutsuttaessa koko ohjelma kaatuu (Unixissa segmentation fault). Tämä johtuu siitä, että funktio päätyy kutsumaan itseään loputtomiin (päättymätön rekursio): Aiempien kutsukertojen muuttujat [2] kuluttavat muistia, kunnes se yksinkertaisesti loppuu.

Rekursiolla saa aikaan toistoa. Periaatteessa mikä tahansa toistorakenne (silmukka) voidaan korvata rekursiolla. Parhaiten rekursio sopii kuitenkin sellaisten ongelmien ratkaisuun, jotka ovat luonteeltaan rekursiivisia. Niitä voidaan “luonnollisesti” yksinkertaistaa siten, että jäljelle jäävät osaongelmat ovat alkuperäisen ongelman yksinkertaistettuja tapauksia.

Usein rekursiivinen ratkaisu on lyhyempi ja siistimpi kuin vastaava silmukkarakenteella toteutettu ratkaisu. Toisaalta, yleensä rekursiivinen ratkaisu on ainakin hiukan hitaampi ja kuluttaa enemmän muistia kuin silmukkarakenne.