Function pointers¶
When talking about programming languages, we often mention that the programs include data and functions. However, the division is not quite this straightforward. The functions can be data as well.
You might hear the phrase ”functions are first class citizens”. This means that you can operated with functions in the same way you do with the other data elements. You can, for example, pass a function as a parameter to another function, pass it as a return value of a function, or store it into a variable. In C++, you can do all this with the so-called function pointer.
A function taking another function as its parameter or returning another function is called a higher-order function. Functions that are not higher-order ones can be called as first-order functions.
Numeric integration¶
Let us study an example that you can find in the directory
examples/10/integral.
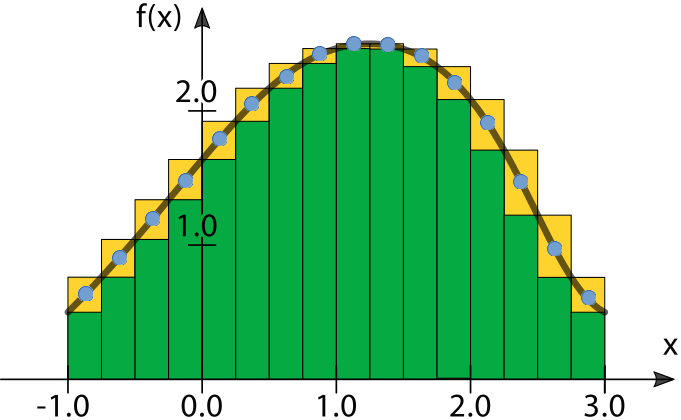
The idea of numeric integration is to approximate the area between the graph of a function and the X-axis by dividing the area into narrow, rectangular areas, and calculating the sum of these rectangular areas.
In the illustration above, you can see two different ways of approximating the area between the graph, drawn in black, and the X-axis. The result of calculating the sum of the areas of the green rectangles is a lower sum of the approximate value of the area. The yellow rectangles are partly hidden behind the green ones, but by summing their areas we can get the upper sum for that same approximate value of the area. We could get a closer approximate value by increasing the amount of rectangles (i.e. by decreasing their widths).
In our example program, we do not calculate the lower sum or the upper sum. Instead, the height of a rectangle is defined by the value of the function at the center of the rectangle. In the illustration, these points are marked with blue dots.
The example program implements the function integrate, the first
parameter of which is the function f that we want to integrate:
double integrate(Func f, double left, double right, int number_of_partitions = 500);
The implementation of the function uses the definition
using Func = decltype(&polynomial);
The command decltype reveals the data type of any variable or function.
We also could use the type definition syntax of C++ for the definition
using Func = double(*)(double);
meaning, Func is a pointer to a function that returns a double and
also gets a double as a parameter.
The first double in the definition is the return value, (*) means the
function pointer, and within the parentheses, there is the list of parameters.
Certainly, it would be possible to leave out the statement using, and
to define the function integrate in the following way:
double integrate(double(*f)(double), double left, double right, int number_of_partitions = 500);
Please note that we do not simply replace the
identifier Func with the contents of the right side of the assigning
operator in the statement using.
Pay attention to where the name of the function pointer f is written.
When we call the function integrate, we must give it a pointer to a
function as a parameter, like below:
cout << integrate(sin, 0, 2) << endl;
cout << integrate(cos, 0, 2) << endl;
cout << integrate(sqrt, 0, 2) << endl;
cout << integrate(polynomial, 0, 2) << endl;
Please note that the examples above do not have parentheses after the first parameter, because they are not function calls, they are pointers to a function.
Purposes of function pointers¶
We will get back to function pointers during the next rounds. Function pointers are useful, for example, in the following situations:
- We want to choose the functionality to be executed in a program,
but we do not want to include a very long
ifstructure, with each block containing one of the possible functionalities (see the exampleexamples/04/datadrivenprogrammingand material at Data driven programming from round 4). - We are implementing graphical user interfaces and we want to bind a functionality to a component of the user interface.