Recursion in general¶

Recursive functions: factorial example¶

Usually, recursion in the context of programming is related to functions. [1] A recursive function is self-defined, meaning it calls itself.

Let us implement the aforementioned factorial calculation with a recursive C++ function:

unsigned int factorial(unsigned int n) {
    if ( n == 0 ) {
        return 1;
    } else {
        return n * factorial(n - 1);
    }
}

which calculates and returns the factorial of its parameter n.

Basically, you can write the function straight from the recursive definition of factorial, but it is far more useful to understand how the function works, and why it produces a correct result.

Let us presume you call the function factorial like this:

int main() {
    cout << factorial(5) << endl;
}

and examine, stage by stage, how the execution proceeds. After the main program has called the function, the program executes the body of the function factorial defined above. The situation seems like below:

The covered main box in the picture means that the execution of the main function is not finished. First, the factorial function covering main has to execute the return command, and only after that, the execution of main can continue from the point where factorial was called.

Because the value of n is 5, the program executes the else branch.

Before factorial is able to return a value, it must calculate a value to the expression n * factorial(n - 1). Therefore, the execution of factorial remains unfinished until the recursive call factorial(n - 1) finishes calculating the factorial of 4.

In fact, the execution of this recursion round is identical to the one before, except that the value of the parameter n is now 4:

The execution, again, goes to the else branch, and the recursion advances deeper and deeper. Take note of the unfinished executions of the factorial function increasing in the background.

The program will continue like this, until the value of the parameter n reaches 0:

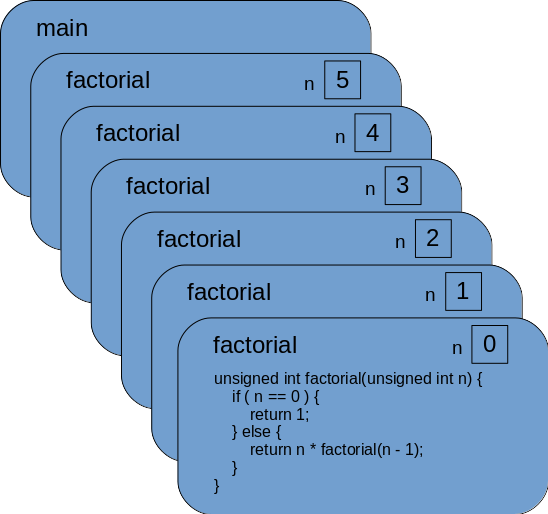
Now, instead of the recursive call, what happens is that factorial returns the value 1, and the stack of unfinished function calls starts to be released.

The last recursive call returns the value 1 to the second last call of factorial, and we multiply it by the value of parameter n that is also 1:

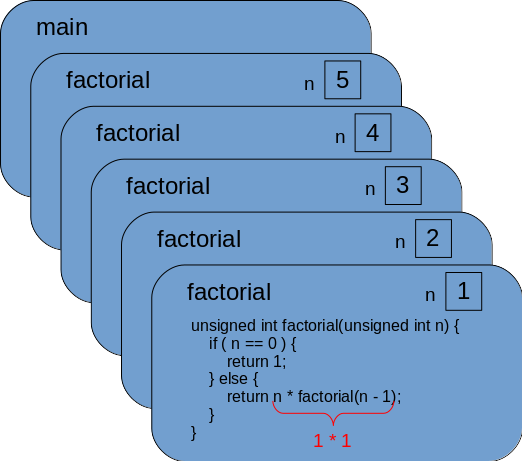
Please note that each call (instance) of the factorial function has its own version of the parameter variable n. The value of n is still the same when we return from the recursively called function to execute the commands of the calling instance. Why?

It is the same with all local variables.

The next unfinished factorial function continues in the same way:

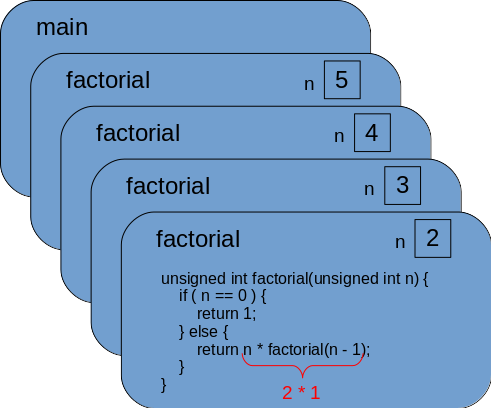
In this way, recursive calls unwind and the execution returns back to the first instance of the factorial function:

It returns the value of the factorial of 5 to the main program:

More examples¶

Materials of this round provide a recursive versio for number series game: examples/06/recursive_number_series_game/.

The example code has also another recursive function. It counts the amount of numbers divisible by 3 or 7 in a certain range.

Conclusion¶

Recursion is nothing special from the programming language’s viewpoint: recursive functions are just functions, just like all the rest. Recursion is difficult to understand because it demands the programmer to perceive the problem and its solution in a possibly nonintuitive (?) way.

It is easier to design and understand recursive functions when you remember the following facts:

• A function is recursive if it calls itself (directly or indirectly).
• During the execution, as many instances of the recursive function are ”on” as there are unfinished recursive calls.
• Each instance has its own values for the parameters and local variables.

Recursive function has two essential characteristics you should remember:

1. It has to have a terminating condition (or several) that recognizes the trivial cases of the problem and reacts to them without having to make a new recursive call.
2. Each recursive call has to simplify the problem in question in order to finally reach the trivial case.

The previous was represented in the factorial function like so:

1. The condition of the if structure (n == 0) is a trivial case: We know the value of zero’s factorial right away.
2. Each recursion round was considering the factorial of a number smaller by one: The call parameter decreased by one.

If you forget either of these, the whole program will crash when you call the function (segmentation fault in Unix). The reason for that is that the function ends up calling itself indefinitely (an infinite recursion): The variables of the earlier calling instances [2] use memory until all the memory is used.

Recursion creates repetition. In principle, any loop structure can be replaced with a recursion. The best use of recursion is solving problems that are, by nature, recursive. You can simplify them ”naturally” in a way that the reduced sub-problems are simplified cases of the original problem.

Often, a recursive solution is shorter and cleaner than a corresponding loop structure solution. However, usually the recursive solution is at least slightly slower and uses more memory than the loop structure.