- COMP.SEC.100
- 19. Sovellettu kryptografia
- 19.1 Sovellettu kryptografia - Johdanto
Sovellettu kryptografia - Johdanto¶
Yksi tietoturvallisuuden perustekijöistä on kryptografia. Se on paljon muutakin kuin salausta. Taustalla on useita tieteenaloja matematiikan lisäksi. Päällimmäisinä—tai oikeastaan pohjalta lukien seuraavina ovat teoreettinen tietojenkäsittelytiede sekä ohjelmisto- ja laitteistotekniikka. Näiden lisäksi algoritmien käytännön turvallisuus edellyttää myös käytettävyyttä ja sovellusohjelmoinnin rajapinnan (API) suunnittelua. Koska pohja on näin laaja, harva ymmärtää kaikkia näkökohtia täydellisesti. Muodostuu aukkoja
- teorian ja käytännön,
- suunnittelun ja toteutuksen sekä
- toteutusten ja niitä soveltavien kehittäjien välille.
Nämä aukot johtavat haavoittuvuuksiin. On harvinaista, että standardoidut, laajalti käytetyt kryptoalgoritmit sinänsä epäonnistuvat, kun niitä käytetään oikein. On tavallisempaa, että kryptografia murtuu epäsuorista syistä. Sellaisia ovat esimerkiksi API-kirjastoliittymän virheellinen käyttö, huono avaintenhallinta, perusalgoritmien turvaton yhdistely monimutkaisessa järjestelmässä tai jokin sivukanavavuoto. Tämän kappaleen aiheet ovat esillä tässä sovelletun kryptografian luvussa, jossa teoriaa käsitellään vain sen verran, että ilmiöt voi ymmärtää. Luonnollisesti kyseiset asiat itsekin kuuluvat osaamistavoitteeseen. Teoreettiset seikat tulevat esille kursseilla Kyberturva 2 ja Cryptography Engineering. Tämän materiaalin lyhyt kryptoteorian luku esittelee muutamaa aihetta esimerkinomaisesti.
Terminologinen huomautus. Autentikoinnista käytetään tässä materiaalissa yleensä suomenkielistä termiä todennus mutta ei tässä kryptologisessa pääluvussa. Tässä todentaminen tarvitaan käännökseksi termille verifiointi, ja se koskee allekirjoituksia (ja eheyskoodeja). Allekirjoituksen verifiointi on siis todentamista eikä siinä ole kyse autentikoinnista.Kryptoalgoritmit, -systeemit ja -protokollat¶
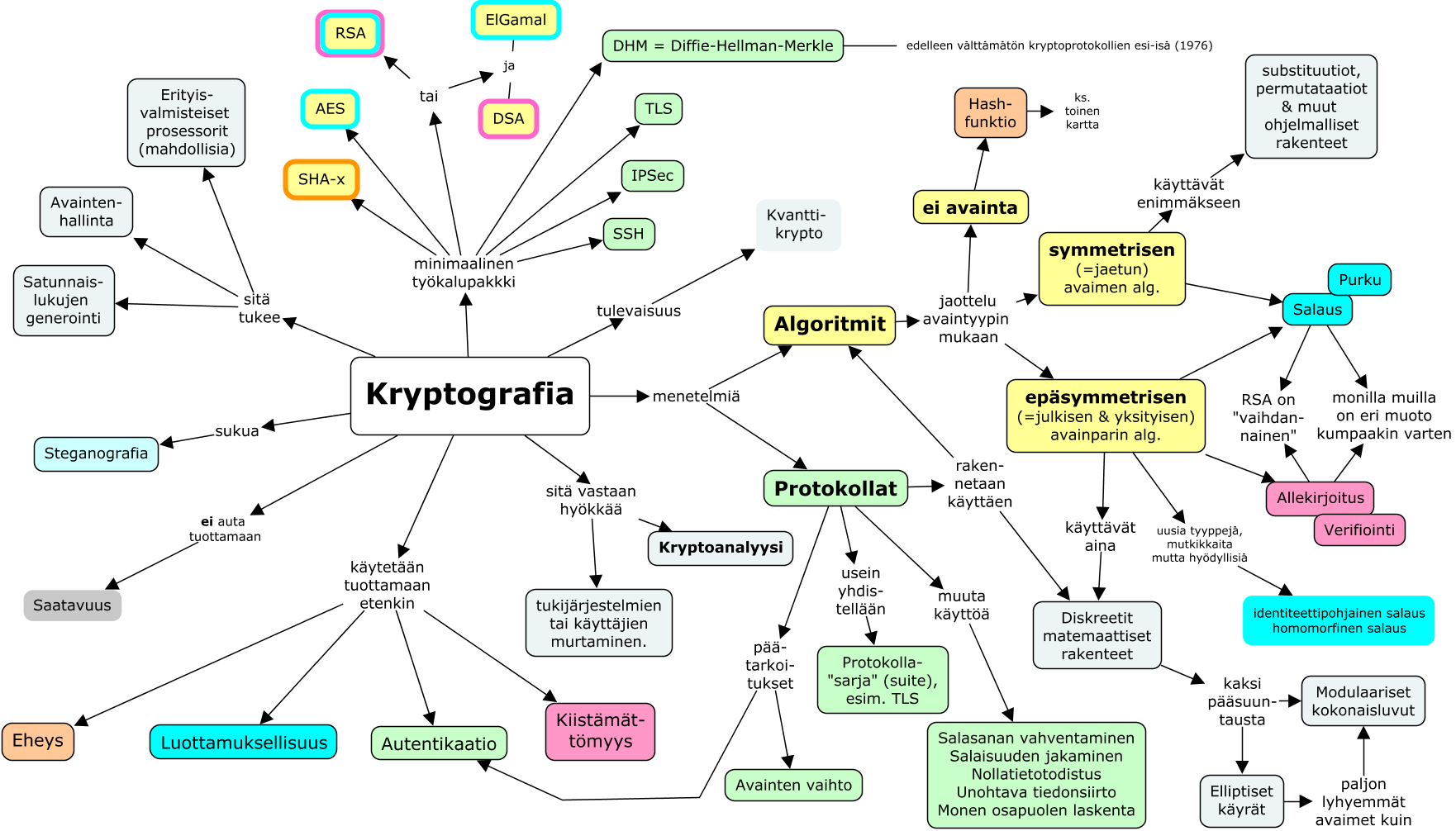
Algoritmit ovat kryptografian ytimessä. Jäljempänä niitä on ryhmitelty primitiiveiksi, joita toisinaan kutsutaan skeemoiksi (schemes) tai kryptosysteemeiksi. Esimerkiksi julkisen avaimen salaus, PKE-skeema (public key encyption) koostuu kolmen algoritmin kokoelmasta: avainten luonti, salaus ja salauksen purku. Kun tutustut erilaisiin tiedonlähteisiin, huomaat vaihtelua termien rajauksissa. Algoritmi, skeema, primitiivit ja jopa protokollat menevät päällekkäin, ja niitä käytetään joskus toistensa vaihtoehtoina. Tässä alaluvussa tuodaan esille yksi jaottelu, jossa otetaan melko vähän kantaa siihen, miten kryptoalgoritmeja käytetään varsinaisen kommunikoinnin osana, eli protokollissa.
Ennen kuin syvennyt algoritmeihin ja protokolliin, kannattaa painaa mieleen, että niiden tehtävänä on viime kädessä muuntaa suurten datamäärien ja transaktioiden suojaamistehtävä muutaman sadan bitin mittaisten avainten suojaamistehtäväksi.
TLS-protokolla
Runsaan teorian konkretisoimiseksi tämän luvun esimerkeissä tarkastellaan TLS-protokollaa. TLS:stä on muuallakin materiaalissa, joten tässä sen käsittely jää aika pinnalliseksi. Kyseinen protokolla on vastuussa päivittäisen tietoliikenteesi salaamisesta, kun yhdistät lähes mille tahansa verkkosivulle. TLS:n läsnäolosta ilmoittaa verkkosivun URL-osoitteen alussa oleva “https://”. Mikäli siinä lukee vain http, ei yhteys ole salattu ja täten kaikki kyseiselle sivulle lähettämäsi data on kenen tahansa yhteyttä seuraavan luettavissa. Tämä on täysin mahdollinen riski esimerkiksi julkisessa kahvilassa tai vaikkapa junassa, mikäli yhdistät salasanattomaan WiFi-verkkoon. Tällöin hyökkääjä ei tarvitse tietoliikenteen vakoiluun muuta, kuin läppärin, halvan USB-antennin ja WireSharkin. (Mikäli edellisen lauseen innoittamana katselet verkkokaupasta Kali Linuxia tukevia antenneja, muista, että tietoliikenteen vakoilu on rikos.)
TLS on siis protokolla, jota tietämättäsi käytät ehkäpä satoja kertoja päivässä. Lisäksi se toimii esimerkkinä hyvin siksi, että se koostuu useasta erityyppisestä kryptoprimitiivistä: autentikointi (julkisen avaimen kryptografiaa), avaintenvaihto sekä symmetrinen salaus. Pääset seuraavaan esimerkkiin tästä
Peruskäsitteet¶
Salakirjoituksen eli salauksen (encryption, ciphering) idea on yksinkertainen: lähettäjä panee viestin “lukkoon” avaimella ja vastaanottaja avaa sen samanlaisella avaimella, joka on esim. 128 bitin jono. Muut eivät saa viestiä selville, koska heillä ei ole avainta ja lukitusalgoritmi on niin monimutkainen, ettei avainta voi keksiä eikä lukkoa muutenkaan saa murretuksi missään järkevässä ajassa.
Lähettäjä ja vastaanottaja voivat olla myös sama olio, joka vain tallentaa viestin eli jonkin tiedon myöhempää käyttöä varten niin, että muut eivät saa siitä selvää. Tiedostokin voi muuttua arvaamattomalla tavalla viestiksi, jos haittaohjelma lähettelee koneen tietoja verkkoon. Henkilöiden tai heidän suoraan käyttämiensä koneiden sijasta osapuolet voivat olla vaikkapa tietoverkossa sijaitsevia reitittimiä.
Yleinen mekaanisiin lukkoihinkin pätevä periaate on, että algoritmia ei voi olettaa salaiseksi vaan ainoastaan avain on salainen. Tämä on Kerckhoffsin periaate 1800-luvulta, mutta vakiintui kryptologiaan vasta 1970-luvulla. Jos avain on lukittaessa ja avattaessa sama, järjestelmää sanotaan symmetriseksi, muussa tapauksessa epäsymmetriseksi (asymmetric). Bittimaailmassa epäsymmetria on mahdollista diskreetin matematiikan avulla ja se toteutuu vieläpä niin, että toiseen suuntaan käytettävä avain voi olla julkinen. Vastakkaisen suunnan avainta sanotaan tuossa yhteydessä yksityiseksi, mikä tarkoittaa enemmän kuin että se on salainen.
Julkista avainta ei välttämättä käytetä ennen yksityistä — siinä mielessä kuin salaus tapahtuu ennen purkamista. Jos aluksi käytetään yksityistä avainta “salaamaan” tietoa ja kuka tahansa voi käyttää julkista avainta tiedon “purkamiseen”, ei saavuteta luottamuksellisuutta vaan jotain muuta. Sopivilla julkisen avaimen hallinnointiin liittyvillä järjestelyillä tuloksena on protokollia, joilla saavutetaan kiistämättömyyttä ja autentikointia. Julkisen avaimen algoritmien kannalta kyse on tällöin digitaalisesta allekirjoituksesta.
Avaintenhallinnan lisäksi algoritmit, joilla salataan, puretaan, allekirjoitetaan tai todennetaan allekirjoituksia, tarvitsevat rinnalleen tiivistealgoritmeja ja kryptografisesti vahvoja satunnaislukujen generaattoreita. Kaikki nämä algoritmit yhdessä kattavat kutakuinkin kokonaan kryptografisten algoritmien käsitteen. Satunnaislukugeneraattorit kuuluvat joukkoon, koska niitä tarvitaan erityisesti hyvien avainten luomisessa. Avaintenhallinta ei kuulu joukkoon, koska siinä enintään hyödynnetään kryptografiaa.
Miten kryptisyys toteutetaan¶
Kryptoalgoritmin pitäisi tuottaa “kryptisiä” bittijonoja eli sellaisia, joista asiattomat eivät saa mitään selvää. Hyökkäystä kryptoalgoritmia vastaan sanotaan kryptoanalyysiksi tai murtamiseksi. Algoritmin tavoitteista ja tyypistä riippuu, mitä murtaminen kulloinkin tarkoittaa, esim. halutaanko tietää, mitä viestissä sanotaan, vai lisäksi, millä avaimella se on salattu. Murtomenetelmiä on monenlaisia, mutta ne jätetään myöhemmille kursseille. Tässä vaiheessa on silti hyvä ymmärtää, millä tavoin murtajan tehtävää hankaloitetaan.
Salausalgoritmeissa sovelletaan kahta perusideaa, jotka on kätevä muistaa englannin kautta: “diffusion and confusion”. Näillä tarkoitetaan keinoja, joilla selvätekstin (plaintext tai cleartext) redundanssia (toisteisuutta) kätketään, kun se algoritmissa muunnetaan salatekstiksi eli kryptotekstiksi (cryptotext tai ciphertext). Konfuusio hämärtää selvä- ja salatekstin välistä yhteyttä suorittamalla korvauksia — yksinkertaisimmillaan. Diffuusiossa puolestaan hajotetaan selvätekstin jakaumia koko kryptotekstiin permutaatioiden avulla — taaskin yksinkertaisimmillaan. Kumpikin operaatio on käännettävissä, joten salatekstin purkaminen onnistuu, vaikka näitä operaatioita olisi toistettu eli iteroitu useita kierroksia. Iterointi pitää tietysti tehdä vuorotellen, sillä kaksi peräkkäistä permutaatiota ei ole sen kummempi kuin yksi järjestyksen vaihto, ja vastaava koskee korvauksia.
Edellä mainitut kaksi sekoitusperiaatetta tulevat selvimmin esille lohkosalauksessa, jossa algoritmia sovelletaan yhteen viestilohkoon eli kiinteään määrään viestibittejä kerrallaan. Kyseessä on siis funktio, jolla on parametrina avain ja joka muuntaa jokaisen n-bittisen jonon joksikin toiseksi samanmittaiseksi. Pidentäminen olisi tilan haaskausta ja lyhentävää funktiota taas ei voisi kääntää. Kompressio ennen kryptausta on eri juttu — ja varsin suositeltava, koska se vähentää selvätekstin redundanssia. Tyypillinen n eli lohkon koko on 128.
Oheisessa kuvassa sovelletaan yksinkertaista lohkoalgoritmia viiden tavun mittaiseen selvätekstiin. Avaimena tässä on (tai sellaiseksi voidaan tulkita) nelikko (2-5-4-1-3, 1, 3, 2). Nelikon ensimmäinen alkio ilmaisee permutaation (yhden 120 mahdollisesta), kaksi seuraavaa siirtojen pituudet ja neljäs kierrosten lukumäärän.
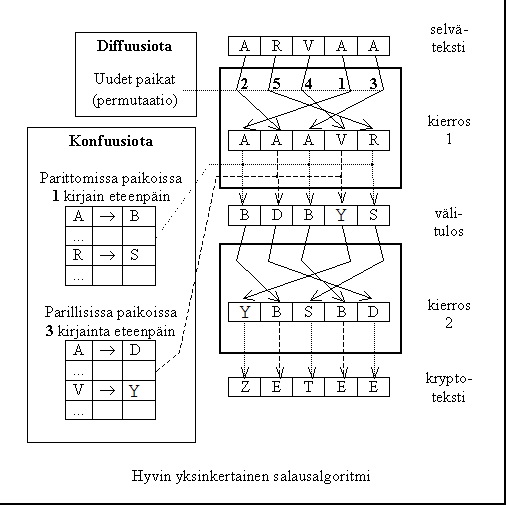
Lohkoalgoritmilla salattaessa ajetaan siis aina yksi tekstilohko kerrallaan koko algoritmin läpi. Algoritmin käyttötavasta (moodista) riippuen tekstinä voi tosin olla muutakin kuin pelkkää selvätekstiä tai ei lainkaan sitä.
Primitiivien jaottelu¶
Primitiiveinä kryptografiassa niin kuin muillakin aloilla voidaan pitää sellaisia asioita, joista kaikki muu voidaan muodostaa, mutta joita ei voi muodostaa toisistaan. Seuraavassa on yhdenlainen kryptoprimitiivien luokittelu.
- Avaimettomat:
- tiivistefunktiot (hash functions; esim. MD5, SHA-*). Perusidea: jos vastaanottaja laskee viestistä tiivisteen ja saa saman kuin lähettäjä uskottavasti väittää, niin viestiä ei ole matkalla muutettu. Murtamisen perusmalli olisi siis samaan tiivistyvän viestin keksiminen.
- Yksisuuntaiset funktiot, jotka voivat olla bijektioita, mutta joita ei pystytä kääntämään, eli ei ole salaluukkua. Keskeinen esimerkki: eksponenttifunktio modulo alkuluku, eli yksisuuntainen permutaatio, joka on Diffie-Hellmanin protokollan perustana.
- satunnaisjonot, eli aidot satunnaisluvut, joita ei pysty ennustamaan edellisten perusteella. Käytännössä taustalle tarvitaan jokin fysikaalinen ilmiö.
- Symmetrinen eli molempiin suuntiin sama avain:
- symmetrisen avaimen salaus: lohkosalaus (block cipher; esim. AES, DES, Blowfish, IDEA, Speck… ; sovelletaan erilaisissa moodeissa: ECB, CTR, CBC, OFB, GCM…) ja vuosalaus (stream cipher; esim. SNOW 3G, ChaCha, A5, RC4…),
- avaimelliset tiivistefunktiot (MAC:t eli message authentication codes, esim. HMAC, CBC-MAC, CMAC): avaimettomien kohdalla mainitun eheyden lisäksi tässä vakuututaan myös viestin lähteen autenttisuudesta.
- (allekirjoitus. Mainittu suluissa siksi, ettei se symmetrisenä takaa kiistämättömyyttä sellaisenaan ilman kolmatta osapuolta),
- näennäissatunnaisjonot (pseudorandom sequences). Avaimena on siemenluku, jota ei saa paljastaa, mutta sitä ei tarvitse myöskään tallentaa. Sen tärkein ominaisuus on mahdollisimman suuri entropia, eli se ettei sitä voi etukäteen ennustaa.
- autentikointiprimitiivit (salasanatyyppiset, myös kertasalasanat).
- Epäsymmetrinen, julkinen avain, jolla on parina yksityinen avain:
- salaus julkisella avaimella (yksisuuntaisen funktion laskeminen), purkaminen 1-suuntaisen funktion salaluukkua käyttäen eli vastaavalla yksityisellä avaimella, joka on salainen. (Esim. RSA, joka on ainoa kommutatiivinen, Rabin, ElGamal, McEliece, elliptisten käyrien kryptosysteemit, NTRU);
- allekirjoitus yksityisellä avaimella (yleensä vain tiiviste allekirjoitetaan), todentaminen julkisella (vastaavat järjestelmät kuin edellä, mutta vain RSA toimii sellaisenaan);
- autentikointiprimitiivit (haaste-vastetyyppiset, erityisesti nollatietotodistus).
Joidenkin menetelmien nimeäminen primitiiveiksi ja rajanveto niiden kesken tai suhteessa ei-primitiiveihin eivät tietenkään ole tarkkoja kuvauksia todellisuudesta, vaan määritelmät ja jaottelut on tarkoitettu vain ihmisen avuksi moninaisuuden käsitteelliseen hallintaan. Primitiivi on tässä joka tapauksessa ymmärretty hieman laajemmin kuin algoritmi, sillä esim. tavalliset autentikointimenettelyt ovat protokollia eivätkä algoritmeja, tai edes skeemoja. Jaottelu vielä laajenee tuonnempana, kun salausalgoritmeihin liitetään viestin autentikointia.
Kryptologian historiasta ja toiminnasta kiinnostuneiden kannattaa lukea Kaisa Nybergin artikkeli Tietojenkäsittelytiede-lehdestä. Artikkeli ei tarjoa vain lisätietoa, vaan siitä saa suoraan tukea myös tässä pääluvussa esitettyjen asioiden ymmärtämiseen.
Kerta-avainjärjestelmä (one-time pad)¶
Tässä alaluvussa esitellään historiallisesti ja teoreettisesti tärkeä mutta epäkäytännöllinen kryptosysteemi, kerta-avainjärjestelmä. Idean näyttää jo Esimerkki 1, mutta esittelyyn on punottu johdattelua useisiin muihin aiheisiin.
Bittien välistä operaatiota XOR (eli eXclusive OR, ‘poissulkeva tai’) merkitään yleensä rengastetulla plussalla ⊕, mutta kirjoitetaan tässä pelkkä +. Tällöin 0+0 = 1+1 = 0 ja 0+1 = 1+0 = 1. Kyseessä on siis samalla yhteenlasku modulo 2.
Esimerkki 1. Olkoon viestinä eli selvätekstinä jono bittejä p = 1010110…; ja avain k = 0110101…; Kryptoteksti c lasketaan biteittäin XOR-summana: c = p + k = 1100011…; Kryptotekstistä c saadaan helposti takaisin selväteksti p XOR-summaamalla siihen biteittäin avain k:
c+k = (p+k)+ k = p + (k + k) = p + 0-jono = p.
Jos edellä avain k oli tosiaan kokonaan keksitty esim. lanttia heittämällä, niin kyseessä oli “one-time pad” eli kerta-avainjärjestelmä. Se (ja muunnelmat) on ainoa salausalgoritmi, joka säilyttää luottamuksellisuuden täydellisesti. Avain on siis satunnainen, sen pituus on sama kuin viestin ja kryptoteksti = viesti XOR avain. Oleellista on että kukin avainbitti tulee käyttöön vain kerran.
Kerta-avainjärjestelmiin viitataan joskus nimellä Vernam-cipher, sillä Gilbert Vernam oli toinen sen keksijöistä vuonna 1917. Silloinen järjestelmä muunsi tekstiä kirjain kerrallaan laskemalla avaimen ja selvätekstin kirjaimia (järjestyslukuja) yhteen modulo 26. Tällainen kirjainten siirto on samanlaista kuin klassisessa Caesarin järjestelmässä, mutta siinä siirto oli aina vakio (3) eikä kätkenyt sen enempää kuin ROT13 (=13 pykälän vakiosiirto), jota on käytetty esim. elokuvaspoilereiden kätkemiseen.
Kerta-avainjärjestelmä on hyvä vain luottamuksellisuuden kannalta. Eheyttä ei saavuteta lainkaan, eikä pelkällä salauksella yleensäkään kovin hyvin. Nämä asiat ovat tekemisissä keskenään. Kerta-avaimella salatun tekstin murtaja ei voi periaatteessakaan tietää selvätekstistä mitään (paitsi pituuden), jos ei tiedä avainta. Samaa salatekstiä vastaa nimittäin sopivalla avaimella mikä tahansa selväteksti. Vastaavasti, oikea vastaanottaja ei pysty havaitsemaan salatekstiin tehtyjä muutoksia. Viestin kaappaaja voisi tietysti vain sotkea sisällön, mutta jos hän sattuisi tuntemaan viestissä olevaa vakiorakennetta, niin sopivalla muutoksella salatekstiin hän voisi muuttaa esim. jonkin tärkeän numeron toiseksi eikä vastaanottaja osaisi epäillä mitään.
Esimerkki 2. Pitkää avainta on hankala käsitellä. Mitä tapahtuu, jos avaimessa olisikin toistoa? Olkoon toistettavana k1 = 0110101, jolloin koko avain olisi 0110101 0110101 0110101 0110101… . Viesti voidaan pilkkoa k1:n mittaisiin lohkoihin p = p1p2p3…. Kryptoteksti koostuu myös lohkoista c=c1c2c3…, missä ci = pi+k1. Koska jokaisessa lohkossa on samat avainbitit, ne eliminoituvat täysin, kun kryptolohkoja summataan pareittain: c1 + c2 = p1 + p2 jne. Kryptoanalyytikolta ei kulu kauaakaan selvittää selvätekstiä p tilastollisilla analyyseilla, sillä varsinkin luonnollisen kielisissä viesteissä on runsaasti redundanssia—eli sitä samaa “ylimäärätietoa”, jonka ansiosta käsin kirjoitetusta tekstistä saa yleensä selvää, vaikka mistään yksittäin nähdystä kirjaimesta ei ehkä saisikaan, jos muut on pyyhitty pois sen ympäriltä. (vrt. myös “Cmadbrigde”) Tilastollinen analyysi on yleisemminkin kryptoanalyysin työvälineitä.
Esimerkki 3. Jotain muuntelua voisi järjestää avaimelle k1 = 0110101, jotta äskeiseltä ongelmalta vältyttäisiin. Muodostetaan “pseudoavain” k = k1k2k3… seuraavasti: ki+1 = luvun a×ki seitsemän alinta bittiä, missä a on jokin k1:stä riippuva vakio, vaikkapa a = k1. Saadaan k = 53, (2809 ==>) 121, (6413 ==>) 13, (699 ==>) 49… eli binäärijonona k = 0110101 1111001 0001101 0110001… . Seitsemän alimman bitin ottamisen voisi ilmaista hienommin jakojäännöksenä modulo 128 (=27). Vastaavaa menettelyä käytetään näennäissatunnaislukujen muodostamisessa, joskaan jakajana ei silloin ole kakkosen potenssi.
Äskeinen avainta “venyttävä” salausperiaate on esimerkki vuokryptauksesta (stream cipher). Käytännössä venytysperiaatteen pitää olla mutkikkaampi (avainvuo, “key stream” vaikeammin arvattavissa) ja lähtökohtana olevan avaimen tietenkin paljon pitempi (esim. 128 bittiä).
Kerta-avainjärjestelmässä avaimen myöhemmät bitit eivät saa millään tavoin riippua edellisistä. Tämä tekee järjestelmästä epäkäytännöllisen. Aivan samalla idealla voi kuitenkin kehittää toisenlaisen kryptosysteemin, jolla on käyttöä. Ajatellaan, että selväteksti p on jonkin tärkeän palvelun salasana, ja se pitäisi tallentaa turvallisesti unohtamisen varalta. Generoidaan samanmittainen satunnaisjono k, ja lasketaan c = p+k. Tallennetaan k ja c kahteen turvalliseen paikkaan. Jos p unohtuu, mutta muistetaan missä k ja c ovat, saadaan niistä p = c+k. Jos hyökkääjä löytää vain k:n tai c:n, hän ei saa mitään tietoa p:stä. Kyseessä on yksinkertaisin esimerkki salaisuuden jakamisesta (secret sharing).
Tästä alaluvussa esiteltiin useita käsitteitä: XOR, kerta-avain, Vernam-cipher, redundanssi, tilastollinen analyysi, vuosalain, näennäissatunnaisjonot, salaisuuden jakaminen. Mainitsematta jätettiin informaatioteoreettinen turvallisuus = “hyökkääjä ei saa mitään tietoa”.
Tiivistefunktiot¶
Bittien “sormenjälki䔶
Tarkistussumma (checksum) on erikoistapaus tiivistefunktiosta (hash function). Se puolestaan on eri asia kuin “kompressio”-tiivistäminen, jossa alkuperäinen tieto voidaan palauttaa joko täysin (ZIP, GIF ym.) tai likimääräisesti (JPEG ym.)
Tutuin esimerkki tarkistussummasta on henkilötunnuksen viimeinen merkki, joka on laskettu muista merkeistä. Vastaava merkitys on pankkisiirron viitenumeron viimeisellä numeromerkillä. Tällaisten tarkistussummien tarkoituksena on näppäily- ym. virheiden havaitseminen. Kansainvälisessä pankkitilin numerossa IBAN:ssa on kaksi tarkistusmerkkiä: kaksi numeroa heti kaksimerkkisen maakoodin jälkeen. Aiemmin loppuosaa voitiin käyttää kansallisena tilinumerona ja siihen sisältyi yksi tarkistusnumero.
Yksinumeroinen tarkistussumma voitaisiin muodostaa summaamalla kaikki numeromerkit ja ottamalla tulokseksi summan viimeinen numero. Näin lasketaan esim. pariteettibitti, joka näkyy tietysti 1-bittien lukumäärästäkin. Yleensä tarkistussumman algoritmi on monimutkainen eikä kyse ole pelkästä summaamisesta. Esimerkiksi CRC:n (eli Cyclic Redundancy Check -menetelmän) ideana on lisätä bittilohkon perään tietty määrä (16 tai 32) bittejä siten, että tulos on jaollinen annetulla kiinteällä luvulla. Jos vastaanottaja ei saa jakoa tasan, lohkossa tai tarkistussummassa (eli FCS:ssä, Frame Check -Sekvenssissä) on tapahtunut muutos. Tämäkin menetelmä mainitaan T. Vuoren laajassa tarkistusmerkkien esittelyssä. Siitä ilmenee myös, miten moninaisissa yhteyksissä tarkistuksia käytetään.
Kryptografinen tiiviste¶
Aktiivisia uhkia vastaan yksisuuntaiselta tiivistämiseltä vaaditaan kryptografista kätkemistä. Se tarkoittaa esim. sitä, että haittaohjelma ei voi viilata saastuttamaansa tiedostoa sellaiseksi, että se tuottaisi saman tarkistussumman kuin alkuperäinenkin. CRC:lle se olisi helppoa. Kryptografisesti vahvat tiivistefunktiot ovat sellaisia, että saman esim. 128-bittisen tiivisteen tuottaminen kahdesta eri tiedostosta on mahdollista vain raa’alla voimalla eli kokeilemalla luokkaa 264 oleva määrä vaihtoehtoja. Syntymäpäiväparadoksin mukaan tämä määrä kokeiluja—mahdollisten tiivistearvojen kokonaismäärän neliöjuuri—riittää nostamaan onnistumisen todennäköisyyden 50%:iin.
Jo 1990-luvun alkupuolella kehitetyt algoritmit MD5 (message digest) ja SHA (secure hash algorithm) ovat 128-bittisiä. Ne ovat edelleen tunnettuja, mutta kummastakin on löydetty heikkouksia (etenkin törmäykset v. 2004 ja 2005). Aiempi suositus näiden tilalle oli 160-bittinen SHA-1 ja nykyään sitäkään ei suositella, vaan pitäisi käyttää SHA-2 -algoritmeja. Niitä on eri pituisia, esim. SHA-256 ja SHA-512 ja näistä katkaisemalla saadut lyhyemmät versiot. Jo vuonna 2012 on standardoitu uuden “sukupolven” SHA-3 -algoritmiperhe. Se on nimeä lukuun ottamatta täysin eri sukua, eli sen sisäinen rakenne poikkeaa aiemmista, joissa puolestaan oli samantapainen rakenne.
Edellä mainittu tiedostojen eheystarkistus on tärkeä mutta melko “pieni” sovellusalue kryptografisille tiivisteille verrattuna etenkin digitaalisiin allekirjoituksiin. Niissä tiivisteet toimivat keskeisinä “avustajina”, eivät sinänsä allekirjoitusoperaatioina. Kryptotiivisteitä käytetään monissa protokollissa, joko kertaalleen tai iteroituina. Esimerkkejä jälkimmäisestä ovat kertakäyttöisten salasanojen ja muiden avainten johtaminen sekä lohkoketjut. Iterointi on sitä, että tiivisteestä lasketaan tiiviste ja siitä tiiviste jne. Erityinen “pieni” mutta äärimmäisen tärkeä käyttökohde on se, että kiinteitä salasanoja ei tallenneta palvelimelle sellaisinaan vaan yksisuuntaisesti tiivistettyinä.
Kryptografisen tiivistefunktion syötteenä voi tekstin lisäksi olla avain. Jos se on kahden osapuolen yhteinen salaisuus, avaimellisen tiivisteen avulla vastaanottaja voi todeta, että teksti on säilynyt eheänä turvattoman yhteyden yli kulkiessaan. Tällainen tiivisteen sovellustapa on hyvin tavallinen protokollissa, esimerkkinä IPsec. Avaimellisesta tiivisteestä käytetään nimitystä MAC, ‘message authentication code’ (ks. lisää). Avaimen mukanaolosta huolimatta yleisesti käytetyt tiivistealgoritmit sinänsä eivät käytä avainta, vaan avain syötetään niille osana tekstiä (esim. tekstin alussa ja/tai sen lopussa). Avaimettomia tiivisteitä kutsutaan toisinaan nimellä MDC, ‘modification detection code’.
Avaimettomiin tiivisteisiin törmää helpoimmin TLS:n tai SSH:n yhteydessä, kun selain tai SSH-ohjelma näyttää (itselleen) tuntemattoman kohdekoneen julkisen avaimen (SSH) tai sen varmenteen (TLS) tiivistettä käyttäjän tarkasteltavaksi. (Juuri niin: avaimesta lasketaan avaimeton tiiviste.) Ihmistä varten bittijonot esitetään tavallisesti heksadesimaalinumeroina, esim. 80 bittiä voivat erottimien kera näyttää tältä 5a:08:c6:21:3c:45:e9:0d:f8:bb.
Tiivistefunktion yksisuuntaisuudesta¶
Kryptografisen hash-funktion tarkoitus on tuottaa viestistä “tiivistelmä”, joka edustaa koko viestiä sikäli, että on vaikea löytää mitään muuta viestiä, jolla olisi sama tiiviste. Koska tiivisteen pituus on vain joitain satoja bittejä ja viesti voi olla miten pitkä hyvänsä, on tietenkin olemassa astronominen määrä viestejä, joista tulee sama tiiviste. Oleellista on, ettei yhtään niistä pysty löytämään. Tätä korostetaan joskus käyttämällä termiä yksisuuntainen tiivistefunktio. Käytännön yhteyksissä käytetään myös nimityksiä digital fingerprint tai message digest (MD).
Tiivistefunktiolta H edellytetty yksisuuntaisuus merkitsee siis sitä, että kun on annettu mahdollinen tiivistearvo h, ei voida millään kohtuullisella vaivalla löytää x:ää, jolle olisi H(x)=h. Usein vaaditaan enemmän: ei saisi löytyä yhtään paria viestejä, jotka “törmäävät” eli tiivistyvät samaksi h:ksi—joko niin, että vaatimus koskee mitä tahansa h:ta tai (vähän lievemmin) niin, että mitään annettua x:ää kohti ei saa löytyä (eri) y:tä, joka toteuttaisi ehdon H(x)=H(y). Mikä tahansa törmäys voi olla vaarallinen, koska sitä kautta voidaan ehkä löytää viimeksi mainitun kaltainen ja päästäisiin esim. huomaamatta korvaamaan allekirjoitettu viesti toisella.
SHA-2 -algoritmiin asti tavanomainen tapa rakentaa hash-funktio oli käyttää “kutistusfunktiota”, joka tuottaa 2n-bittisestä syötteestä n-bittisen tuloksen siten, että jokainen syötebitti vaikuttaa tulokseen. Vaikutus voi olla vieläpä sellainen, että yhden syötebitin muuttaminen vaihtaa keskimäärin puolet tulosbiteistä. Tällaiselle kutistajalle syötetään iteratiivisesti aiempi kutistustulos ja seuraava viestilohko (kummassakin esim. 160 bittiä). Alussa tarvitaan alustusvektori (siis “nollas” kutistustulos) ja viestin täydennys lohkon monikerran mittaiseksi. Useimmiten syötettävän viestin loppuun liitetään sen pituus. Kutistusvaiheen jälkeen voidaan tehdä vielä jokin toisenlainen muunnos. Kutistaja tekee samantapaisia operaatioita (esim. shift ja Xor) kuin lohkosalausalgoritmi, mutta se voidaan rakentaa nopeammaksi, koska ei tarvitse yrittääkään muodostaa käänteisfunktiota. Kuten jo mainittiin, SHA-3 käyttää erilaista rakennetta, joka hyödyntää sienifunktioita (sponge functions). Nimi tulee siitä, että niihin ensin “imetään” selväteksti ja sitten niistä “puristetaan” ulos tiiviste.
Hash-algoritmi on aina deterministinen. Se tuottaa samasta lähtöarvosta saman tuloksen eikä siis sisällä satunnaisuutta. Teoreettisissa tietoturva-analyyseissa hash-funktiot mallinnetaan kuitenkin yleensä satunnaisiksi funktioiksi. Tällaista kutsutaan satunnaisoraakkelimalliksi (random oracle model). Nimen ideana on, että oraakkeli vastaa “mitä sattuu” mutta samaan kysymykseen silti aina samalla tavalla. Tällaisessa mallissa tarkasteltava hyökkääjä ei siis voi käyttää hyväkseen mitään hash-funktiossa todellisuudessa olevaa rakennetta. Puute on teoriassa vakava, mutta käytännön tulokset ovat olleet hyviä. Kohtaat muitakin oraakkeleita, jos opiskelet kryptologiaa enemmän. Sellaisilta voi mallissa esiintyvä hyökkääjä kysyä esim., onko selvätekstissä parillinen määrä ykkösbittejä.
Kartta¶
Allaoleva käsikartta tiivistää ja jäsentää, mitä tiivistefunktioista edellä sanottiin. Joitakin asioita käsitellään tarkemmin tuonnempana, esim. MAC, autentikoitu salaus ja sovellukset protokollissa.
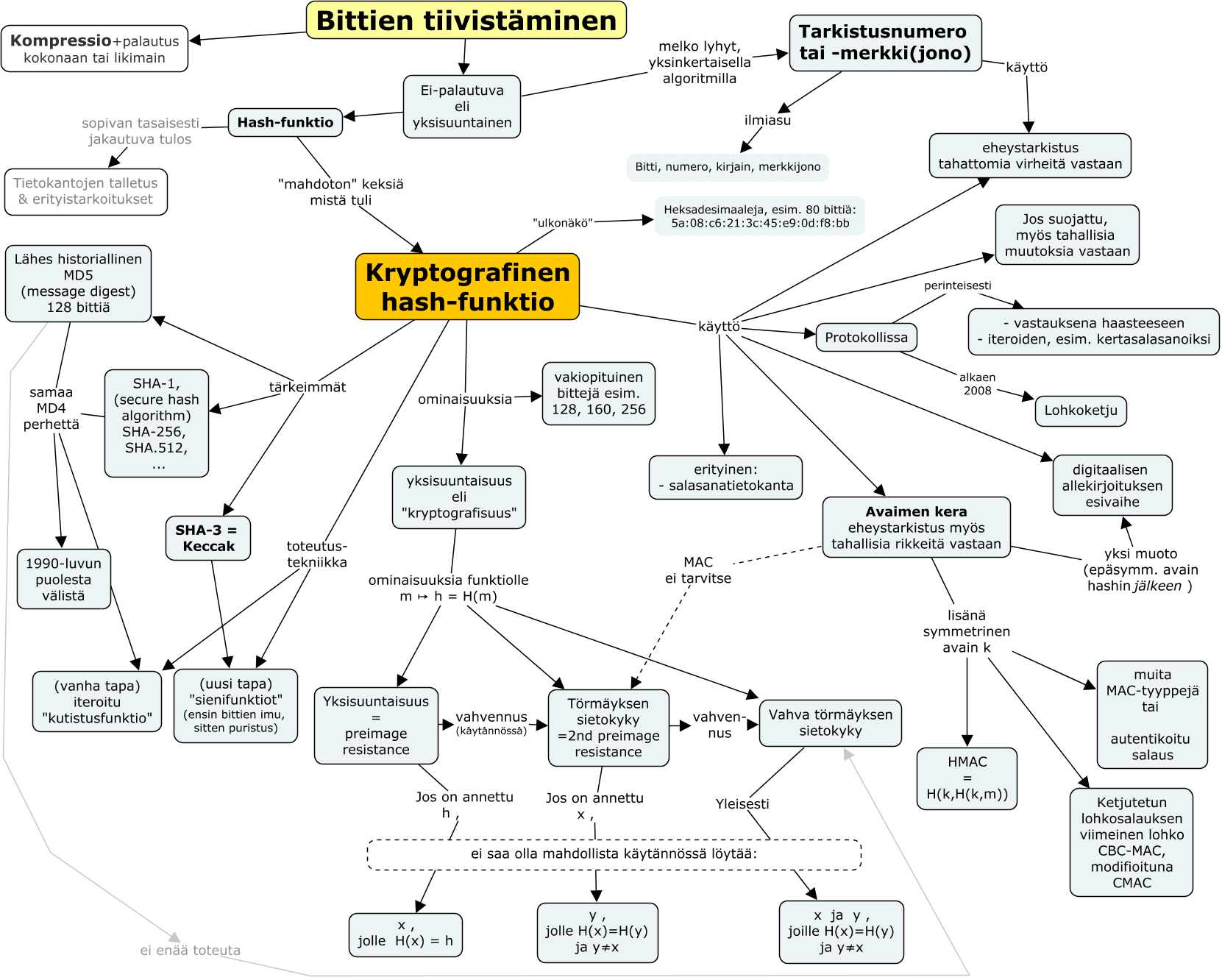
Huomautus käsitekartan saavutettavuudesta.
Lohkosalaimet¶
Algoritmit¶
Salausalgoritmeja on olemassa sadoittain, ja kymmeniä on yleisesti käytössäkin. Jokainen voi kehitellä niitä itsekin, mutta se ei kannata. Asiaan perehtyneet tutkijatkin ovat usein saaneet huomata, että joku toinen on murtanut heidän luomuksensa. Lohkosalaimen teoreettinen turvatavoite kuulostaa silti yksinkertaiselta. Pitäisi tuottaa n-bittisten jonojen avaruuteen avaimesta riippuva permutaatio, jota hyökkääjä ei pysty erottamaan satunnaisesta permutaatiosta. Jos myös avain on n-bittinen, algoritmista muodostuu erilaisia salaimia 2n kappaletta, yksi kutakin avainta kohti. Jokaisen pitäisi muistuttaa jotain satunnaista permutaatiota, joita puolestaan on aika lailla enemmän: (2n)! kappaletta. Tällainen turvallisuuden määrittely kuuluu formaalien analyysien alaan eikä kryptoanalyytikko murtopuuhissaan mieti sitä vaan esimerkiksi sitä, miten hieman toisistaan eroavat selvätekstit etenevät algoritmin läpi.
Edellä peruskäsitteitä käsittelevän luvun algoritmikaavio tarjoaa esimerkin siitä, miten monet lohkosalaimet on tehty. Siinä tehdään kirjainten korvauksia ja sekoituksia ja toistetaan tätä eli selväteksti “epäselvenee” yhä enemmän salaimen läpi kulkiessaan. Esimerkkialgoritmia voisi tässä mielessä tehostaa modifioimalla avainta jotenkin myöhempiä kierroksia varten, ja kunkin kierroksen korvausten ja sekoitusten tuloksia voisi yhdistellä jotenkin mutkikkaammin. Tähän tapaan toimii 1900-luvun viimeisen neljänneksen tunnetuin salausalgoritmi DES, Data Encryption Standard. Se käsittelee 64 bitin lohkoa kahtena puolikkaana, 32 bitin jonoina. Se mm. XOR-summaa toisesta puolikkaasta lasketun funktion ensimmäisen puolikkaan kanssa ennen puolikkaiden vaihtoa seuraavaa kierrosta varten (ns. Feistel-periaate). DES ei ole enää turvallinen, koska sen avaimen pituus on vain 56 bittiä. DES-algoritmille saatiin kauan lisäaikaa käyttämällä sitä kolmesti peräkkäin kahdella tai kolmella avaimella. Menetelmää ei ole pidetty turvallisena moneen vuoteen. NIST-tiedotteen mukaan sitä ei saa enää käyttää vuoden 2024 alusta mihinkään muuhun kuin aiemmin salatun data purkuun.
Korvaajaksi DES:lle kehitettiin vuosituhannen vaihteessa AES, Advanced Encryption Standard. Sen algoritmin alkuperäinen nimi on Rijndael. Lohkokoko on AESissa 128 bittiä ja avain on 128, 192 (=1½×128) tai 256 bittiä. AES on siis lohkosalain ja senkin sisällä tehdään useita kierroksia, 10, 12 tai 14 avaimen pituuden mukaan. Algoritmi ei noudata yksinkertaisten korvausten ja sekoitusten vuorottelua. Joka kierroksella kyllä tehdään ensin korvaus ja sitten permutointi, mutta lisäksi tapahtuu erilainen sekoitus tavumatriisiksi kirjoitetun lohkon kertolaskussa. Joka kierroksella lohkoon XOR-summataan kierrosta varten laskettu funktio avaimesta.
AES on erittäin nopea toteuttaa sekä ohjelmallisesti että kovolla. Avaimen pituuden puolesta AESilla salattujen tietojen arvellaan pysyvän turvassa ohi vuoden 2030. AESin nopea ja turvallinen toteuttaminen on haastavaa ympäristöissä, joissa hyökkääjä voi käyttää samoja muistiresursseja uhrinsa kanssa, esimerkiksi cache-muistia. Silti harvoin tarvitaan muuta lohkosalausta kuin AES, koska sillä on laajasti toteutuksia eri alustoilla eikä siinä ole tunnettuja tietoturva-aukkoja. Yksi poikkeus ovat rajoitetut laskentaympäristöt, joihin voi sopia paremmin esim. Speck.
Lohkosalaimia ei tulisi käyttää tietojen salaamiseen lohko kerrallaan, paitsi erittäin rajoitetuissa olosuhteissa, joissa ei haittaa se, että samanlainen selvätekstilohko tuottaa aina samanlaisen kryptotekstin. Jos samalla avaimella salataan hyvin vähän dataa, haittaa ei esiinny.
Symmetrinen salaus TLS:sä
TLS:sä käytetään sekä symmetrisiä- että epäsymmetrisiä salausalgoritmeja. Syy tähän on se, että vaikka epäsymmetrisellä salauksella pystyisi salaamaan koko lähetettävän datapaketin, on se huomattavasti hitaampaa. Siispä epäsymmetristä salausta käytetään autentikointiin sekä symmetrisen avaimen sopimiseen. Eli toisin sanoen osapuolet (asiakas ja palvelin) sopivat yhteisen salaisuuden salaamalla sen epäsymmetrisesti. Yhteisestä salaisuudesta molemmat osapuolet laskevat samat symmetriset istuntoavaimet. Varsinainen data salataan esimerkiksi AES:llä tai muulla symmetrisellä algoritmilla (katso Autentikoitu salaus).
Reaalimaailman esimerkkinä symmetristä salausta on helppo verrata ihan vain avaimeen ja lukkoon. Ajatellaan, että Teijalla ja Teemulla on yhteinen talletuslokero arvokkaiden golfmailojen säilömiseen. Myös mailat ovat kaverusten yhteisomistuksessa. Kyseisessä lokerossa on vanhanaikainen lukko, joten molemmat osapuolet tarvitsevat saman avaimen. Kunhan avain on molemmilla hallussa, ei mailoihin käsiksi pääseminen ole sen kummempaa. Teemu ja Teija eivät kuitenkaan koskaan pääse näkemään kasvokkain, joten itse avainten vaihtamiseen he tarvitsevat hieman monimutkaisemman operaation, joka käsitellään myöhemmässä esimerkissä
Salausmoodit (syventävä)¶
Tässä esitellään kaksi lohkosalaimen käyttötapaa eli moodia, CBC ja CTR. Kolmas, GCM tulee esille tuonnempana, kun salauksen lisäksi toteutetaan viestin autentikointi. Aloitetaan kuitenkin ECB:llä, joka sekin on moodi.
Johdannoksi pitää oivaltaa, että lohkosalainta voi käyttää yksinkertaisesti salaamalla kukin selvätekstilohko toisistaan riippumatta. Tätä sanotaan elektroniseksi koodikirjaksi (ECB), eikä sitä pidä käyttää kuin hyvin lyhyisiin viesteihin. Tähän jo viitattiin edellä. Oleellista on, ettei salattavaksi päädy samalla avaimella kahta samanlaista selvätekstilohkoa, ainakaan kovin usein. Sellaiset tuottaisivat aina saman kryptolohkon, ja murtaja voisi ruveta laatimaan käänteistä koodisanakirjaa. Ääriesimerkki tällaisesta olisi jokin etänä toimiva kirjoitusohjelma, esim. syöttölomake, jossa jokainen näppäimenpainallus kulkee salattuna palvelimelle ja kaiuttuu takaisin näytölle. Käänteinen koodikirja muodostuisi varsin nopeasti pienellä tilastollisella analyysilla. Esimerkiksi englannin kielellä yleisin kryptolohko olisi “E” ja toiseksi yleisin “T” jne.
Lukiessasi edellä oleva koodikirjahyökkäystä ajattelit jo varmaan torjuntakeinoja. Saatoit keksiä kaksikin ilmeistä tapaa. Salauksen täytyy riippua siitä, miten salattava kirjain tai tekstilohko sijaitsee suhteessa muihin. Tällöin lohkosalaimelle syötetään aina erilaista laskettavaa. Pitää muistaa, että 128 bitin lohkossa riittää vaihtua yksikin bitti ja salateksti tulee täysin erilaiseksi.
Mikä on yksinkertaisin lisätieto, joka voidaan tekstilohkon ohella syöttää salaimelle? Varmaankin se, monesko lohko on menossa. Vastaanottaja tietää saman ja toki hyökkääjäkin. Edellinen pystyy purkamaan vaivatta. Jotta jälkimmäinen ei saisi ilmaiseksi yhtään selvätekstin bittiä, lohkolaskurin arvolle ei varata omaa tilaa selvätekstissä. Sehän vähentäisi salauksen hyötysuhdettakin. Sen sijaan laskurin arvo voidaan summata selvätekstilohkoon ennen salausta. Summaus tehdään tietysti biteittäin XOR-operaatiolla. Vastaanottaja soveltaa kryptolohkoon ensin purkualgoritmia ja sitten XOR-summaa laskurin arvon. Laskurin arvo kumoutuu ja selväteksti tulee esiin.
Edellä luonnosteltiin lohkosalaimen “laskurimoodia”, jonka varsinainen toteutus esitellään tämän jakson lopussa. Toinen tapa ottaa huomioon lohkon sijainti on ottaa bittejä naapurilohkoista mukaan XOR-summalla samaan tapaan kuin laskurin arvo. Pieni pohdinta esimerkiksi kirjain-kerrallaan salauksen suhteen johdattaa kolmeen päätelmään: (1) bittitieto kannattaa ottaa edellisistä lohkoista, ei tulevista ja (2) yhden lohkon bitit varmaan riittävät, mutta ne voi lähes samalla vaivalla käyttää kaikki, (3) jotta ensimmäinenkään kryptolohko ei olisi toiste joltain aiemmalta kerralta, sekin pitää laskea jostain lisätiedosta. Tällaista lisätietoa kutsutaan luontevasti alustusvektoriksi, ja sitä merkitään tässä ja eräissä muissa yhteyksissä lyhenteellä IV, initialization vector. Se pitää kertoa vastaanottajalle selväkielellä, jotta salauksen purku onnistuisi. Hyökkääjälle IV:stä ei ole mainittavaa apua sellaisenaankaan, mutta erilainen sen pitää olla eri kerroilla. Muutenhan 3-kohta ei toteutuisi. Satunnaisuus riittää, koska bittejä on paljon, eli ei tarvitse pitää kirjaa IV-arvoista. Täytyy vain varmistaa, niin tässä kuin muissakin yhteyksissä, että satunnaisuus on riittävän aitoa.
Edellä luonnosteltiin CBC-moodi eli lohkosalaimen ketjutettu käyttö. Jotta saataisiin oikea CBC, eli cipher block chaining, tarvitaan vielä neljäs valinta: (4) edeltävän lohkon käsittelystä seuraavan salaukseen ketjutetaan kryptolohko, ei selvätekstilohkoa. Jälkimmäinenkin olisi purkamisen kannalta mahdollista, mutta se tekisi järjestelmästä samalla tavalla heikon kuin ECB-moodi. Kryptolohkot olisivat yhden selvätekstilohkon sijasta kahden peräkkäisen selvätekstilohkon kuvia. Vertaa tätä Esimerkkiin 2 kerta-avainjärjestelmän esittelyssä.
Lohkosalaimen CTR-moodi eli counter mode soveltaa edellä kuvailtua IV-ideaa siten, että lohkojen laskentaa ei aloiteta ykkösestä vaan IV-arvosta. Toinen—ja varsin dramaattiselta kuulostava—ero alussa johdateltuun laskuri-ideaan on se, että selvätekstiä ei syötetä lainkaan lohkosalaimeen. Salaimella vain kryptataan (IV+laskuri) -lohkoja ja saadaan satunnaiselta näyttäviä lohkoja, jotka XOR-summataan selvätekstilohkojen kanssa. Vaikka IV ei edes ole salainen, sen 128 satunnaista bittiä yhdessä lohkosalaimen ja siinä käytetyn salausavaimen kanssa riittävät tuottamaan murtajan näkökulmasta ennustamattoman bittivirran. Se kelpaa käytännön korvikkeeksi kerta-avainjärjestelmän avaimelle. Vertaa tätä “pseudoavaimeen” Esimerkissä 3 kerta-avainjärjestelmän esittelyssä. CTR-moodi on siis yksi keino avaimen “jatkamiseksi”. Tällainen menettely on kätevä senkin vuoksi, että salaus ja purku voidaan tarvittaessa rinnakkaistaa, tai voidaan purkaa vain tietystä kohdasta. Onhan IV+laskuri -operaatio paljon nopeampi kuin salaimen käyttö.
Vuosalaimet¶
Vuokryptauksessa kryptoteksti saadaan laskemalla XOR-summa selvätekstistä ja samanmittaisesta näennäissatunnaisjonosta, avainvirrasta, joka lasketaan avaintenvaihdossa sovitusta kiinteän mittaisesta avaimesta. Yksi tapa tuottaa tällainen jono on käyttää lohkosalainta. Ensimmäinen avainlohko voidaan laskea, tai siis lohkosalata, jostain vakioarvosta ja jokaista seuraavaa varten kasvattaa syötettä yhdellä tai sitten syöttää avainlohko yhä uudestaan takaisin lohkosalaimeen. (Edellinen tapa on sama kuin lohkosalaimen CTR-moodi, ja jälkimmäinen on sekin lohkosalaimen käyttötapa, jolla on oma nimi, OFB, output feedback mode.)
Vaikka vuosalaus voidaan toteuttaa lohkoalgoritmin avulla, näin ei tehdä silloin kun tavoitellaan suurta salausnopeutta. Perinteisesti nopea vuosalain on toteutettu lineaarisilla takaisinkytketyillä siirtorekistereillä (linear feedback shift registers, LFSR), siis ei ohjelmalla vaan kovolla. Pienten puskureiden tai tiukkojen reaaliaikavaatimusten yhteydessä, esim. telekommunikaatiossa vuosalaus on usein välttämätöntä (vrt. kaapeli-TV:n “scrambler” tai puhelun kryptaus radiotiellä).
Tämä kappale on täydentävää tietoa, joka avaa termit L, F, S, R: LFSR koostuu n:stä yhden bitin rekisteristä (R), joihin on aluksi syötetty alkuarvoiksi avaimen bitit. Kellon antaessa sykäyksen bitit siirtyvät (S=shift) seuraavaan rekisteriin siten, että viimeisestä muodostuu rekisterin ulostulo. Tämä rekisteristä “ulos putoava” bitti syötetään samalla ensimmäiseen rekisteriin (F=feedback), kuitenkin siten, että siihen on XOR-summattu (L=linear) joidenkin muiden rekisterien sisältö. Siirtorekisteri tulostaa tietyn rakenteestaan riippuvan bittijonon, joka toistuu eli on jaksollinen. Sopivasti valituilla takaisinsyöttökohdilla (“taps”, merkityksessä “hanat”; eivät salaisia) jakson pituus on maksimaalinen eli 2n−1, mikä tarkoittaa, että kaikki mahdolliset bittikombinaatiot—paitsi nollajono—esiintyvät LFSR:n tiloina.
LFSR:n alkutilaksi syötetyllä n-bittisellä avaimella valitaan, mistä kohdasta LFSR:lle ominainen jaksollinen bittijono lähtee. Vaikka jono toistuu vasta tähtitieteellisen monen bitin jälkeen, tämä ei auta siihen, että n bittiä paljastunutta avainvirtaa paljastaa kaiken. Yleisemminkin LFSR:n turvaongelmana on sen lineaarisuus. Sitä on häivytetty vuosalaimissa kytkemällä useita LSFR:iä erityisin tavoin toisiinsa. Esimerkiksi GSM:n eli 2. sukupolven matkapuhelinten A5/1-algoritmissa on prosessorin kellon kontrolloimina kolme LFSR:ää, pituuksiltaan 19, 22 ja 23 bittiä.
Kolmannen sukupolven matkapuhelinverkoissa käytetään vuosalausalgoritmia SNOW 3G, jossa on vain 16-osainen LFSR, mutta jokainen rekisteriosa sisältää 32-bittisen “sanan”. Rekisteriin on kytketty tila-automaatti (finite state machine), joka sekoittaa kahdesta rekisteriosasta otettuja sanoja toisiinsa erilaisin summauksin ja AES-tyylisin korvauksin. Tämän tulos XOR-summataan LFSR:n ulostulosanaan, jolloin saadaan 32 uutta bittiä avainvirtaan.
Salauskäytössä (“E”) vuoasalain SNOW 3G esiintyy nimellä UEA2 3G-verkoissa ja nimellä EEA1 4G-verkoissa. Jälkimmäisissä on myös AES-pohjainen EEA2. Vaihtamalla näissä toinen kirjain I:ksi (“integrity”) saadaan sama algoritmi (“A”) autentikointi- ja eheyskäyttöön.
Viestin autentikointikoodi MAC¶
Turvattoman kanavan yli lähetetyn viestin voi joku muuttaa matkalla, vaikka se olisi salattu. Jos viestin mukana on siitä laskettu kryptografinen tiiviste, hyökkääjä tietysti vaihtaa sen tilalle muokatusta viestistä lasketun tiivisteen. Hyökkäys ei onnistu, jos tiivisteen laskuun tarvitaan jokin lähettäjän ja vastaanottajan yhteinen salaisuus. Tämä on ideana viestin autentikointikoodissa eli MAC-koodissa (message authentication code), kuten mainittiin jo aiemmin.
MAC-skeema koostuu muodollisesti kolmesta algoritmista: KeyGen, Tag ja Verify. Ensin luodaan avain, joka pitää tietysti myös saattaa osapuolten tietoon. Toiseksi lasketaan avaimesta ja viestistä “tag” eli viestin avaimellinen tiiviste, suomeksi selkeimmin MAC-koodi (tai vain MAC, mieluummin kuin tag). Todennuksessa (verifioinnissa) käytännössä lasketaan uudestaan MAC-koodi vastaanotetusta viestistä ja verrataan, onko se sama kuin vastaanotettu arvo. Jos ei ole, viestin eheys on särkynyt eikä myöskään tiedetä, mistä se on peräisin. Jos kolmikko (viesti, avain, MAC) todentuu, viesti on eheä ja autenttinen siinä mielessä, että se on sama kuin silloin, kun joku avaimen tunteva osapuoli on sitä aiemmin käsitellyt.
Edellä vain vihjattu MAC-koodin turvatavoite on muodollisesti ilmaistuna vahva väärentämättömyys valitun viestin hyökkäystä vastaan (strong unforgeability under chosen message attack). Se tarkoittaa, ettei avainta tuntematon hyökkääjä pysty laatimaan uutta (viesti, MAC) -paria, vaikka hän olisi nähnyt useita aiempia pareja, jotka on tehty samalla avaimella ja joiden viestin hän on pystynyt valitsemaan.
MAC-skeema voidaan muodostaa avaimettomasta tiivistefunktiosta tai lohkosalaimesta. Yksinkertaisin tapa olisi käyttää kryptografista tiivistefunktiota H ja syöttää sille sekä avain että viesti, esim. peräkkäin asetettuina. Tällaisista skeemoista on löydetty haavoittuvuuksia, joten on päädytty hieman mutkikkaampaan rakenteeseen, nimeltään HMAC, jossa H lasketaan kahdesti. Jos k on avain ja x on viesti, niin HMAC on H( k, t1, H( k, t2, x)), missä t1 ja t2 ovat täytteitä, joilla syötteet pidennetään hash-funktion H lohkon mittaiseksi. Kaavassa pilkulla erotetut syötteet asetetaan toistensa perään bittijonoksi.
(Syventävä) Lohkosalaimesta saadaan MAC-skeema nimeltä CBC-MAC salaamalla viesti CBC-moodissa ja ottamalla MAC-koodiksi viimeinen kryptolohko. Alustusvektoriksi, eli IV:ksi, käy nollajono. Turvallisuutta voidaan parantaa muokkaamalla viimeiseen salaukseen menevää viimeistä viestilohkoa. Tällaista muunnelmaa kutsutaan nimellä CMAC. Muitakin menettelyjä on ja niitä tulee seuraavassa esille yhdistettynä salaukseen. Pelkkä viestin autenttisuus on nimittäin harvoin riittävä turvatavoite.
Autentikoitu salaus (AE) (syventävä)¶
Edellä MAC-koodia motivoitiin sillä, että viestin luottamuksellisuus ei ole tae eheydestä. Kun johonkin järjestelmään asetetaan tietoturvavaatimuksia ja halutaan luottamuksellisuutta tai ehkä mainitaan suoraan salaus, tarkoitetaan yleensä kuitenkin myös autenttisuuden vaatimusta. Riittävien autenttisuus- ja eheystakeiden lisääminen salauksen yhteyteen voidaan tehdä kolmella tavalla:
- ensin salaus ja sitten MAC (MAC lasketaan kryptotekstistä)
- ensin MAC ja sitten salaus (salatuksi tulee myös MAC)
- salaus ja MAC samalla kerralla
Kaikissa MAC tuo lisää pituutta tulokseen. Vaihtoehto 1 on selkein, mutta sekä 1:ssä että 2:ssa on ongelmana se, että vahva turvallisuus edellyttää molemmille operaatioille omaa avainta. Tämä on ollut yksi syy vaihtoehdon 3 kehittämiseen. Toinen on nopeus. Vaihtoehdoissa 1 ja 2 viesti käsitellään kahdesti, vaihtoehdossa 3 vain kertaalleen.
Kaikkia mainittuja vaihtoehtoja kutsutaan AE-järjestelmiksi (authenticated encryption). Usein toteutetaan samalla sellainen järjestelmä, jossa autentikoidaan viestiin liittyvää oheisdataa, jota ei kuitenkaan voida salata. Sellaista dataa voivat olla viestinvälityksessä tarpeelliset otsikkotiedot osoitteineen. Termi tällaiselle järjestelmälle on AEAD, authenticated encryption with associated data.
Tärkein käytännön AEAD on AES-GCM eli lohkosalain AES sovellettuna GCM-moodissa. Tämä moodi, Galois/Counter Mode, siis lisää perus-AESiin autentikoinnin ja käsittelee oheisdatan. Siinä on syötteenä merkitystä sisältävän oheisdatan lisäksi vielä ns. nonce, joka voi olla satunnainenkin. Sen perusvaatimus on kuitenkin olla toistumaton. (Nimen taustaa: “nonce word” on kertakäyttösana ja “for the nonce” tarkoittaa suurin piirtein “täksi kerraksi”). Laskuri kelpaa nonce-arvoksi ja voi olla hyödyksi, kun järjestelmä pitää kirjaa samalla avaimella salatun data määrästä. Huomaa, että sekä nonce että oheisdata kulkevat selväkielisenä. AES-GCM on käytössä 90%:ssa kaikista www:n TLS-yhteyksistä [ks. CyBOK 1.1, sivu 604].
Toinen tärkeä AEAD on ChaCha20-Poly1305. ChaCha on vuosalain, ChaCha20 on sen versio, jossa tehdään 20 kierrosta, ja Poly1305 on MAC-algoritmi. Näissä ei tarvitse huolestua, että tulee monta muutakin numeroyhdistelmää muistettavaksi. Tietysti ChaCha voi joskus tarvita lisäkierroksia mutta Poly1305 saa nimensä siitä, että siinä lasketaan polynomin arvoa modulo alkuluku 2130−5. Tuossa on 130 bittiä ja kaksi jätetään lopuksi pois, joten MACista tulee tavanomainen 128 bittiä. Tässä AEAD:ssä salaus ja MAC tapahtuvat toisistaan erillään, toisin kuin AES-GCM:ssä, jossa operaatiot sujuvat pienillä lisäyksillä tavanomaisen CTR-salausmoodin ympärillä. Nimessä Galois/Counter sana Galois [gal’wa:] tulee 1800-luvun matemaatikosta, jonka mukaan kutsutaan äärellisiä kuntia (finite fields). Mainitut “pienet lisäykset” lasketaan nimittäin kunnassa GF(2128). Tapaat Galois’n kunnat myös AESin yhteydessä, jos jatkat tietoturvaopintoja.
Julkisen avaimen järjestelmä salauksessa¶
Julkisen Avaimen Johdanto¶
Hyvä salausalgoritmi tarkoittaa muunnosta, jota ei voi kääntää ilman suunnatonta vaivaa, ellei tunne salaista avainta. Tällaiset algoritmit käsittelevät perinteisesti kaiken—ja edelleenkin lähes kaiken—datan, jota kryptografisesti suojataan. Nykyaikaisten tietoverkkosovellusten turvaaminen sellaisilla ei kuitenkaan onnistuisi ilman algoritmeja, joissa avain ei olekaan salainen: Tarvitaan myös sellaisia kryptografisia funktioita, joita on lähes mahdoton kääntää, vaikka funktiossa ei olisi mitään salaista.
Tärkein esimerkki tällaisesta funktiosta on potenssiin korottaminen ja jakojäännöksen ottaminen hyvin suuren alkuluvun suhteen. Tämän funktion kääntäminen vaatisi logaritmin laskentaa. Se onnistuisi hyvin, jos laskenta ei olisi modulaarista eli “jakojäännöstettyä” tuon suuren alkuluvun eli moduulin suhteen. Diskreetti logaritmi suurilla luvuilla sen sijaan ei onnistu missään kohtuullisessa ajassa. Tämä nimenomainen funktio tulee käyttöön avaintenvaihdossa, joka on pohjalla lähes kaiken salatun viestinvaihdon aloituksessa (Diffie-Hellman). Katsotaan tässä johdannossa toisenlaista potenssilaskun tilannetta, josta saadaan salaus- ja purkualgoritmi.
Olkoon luku n kahden suuren alkuluvun p ja q tulo, mutta p:tä ja q:ta ei tunneta. Jos korotetaan jokin luku x toiseen potenssiin ja lasketaan jakojäännös luvun n suhteen, niin lopputuloksesta y ja luvusta n ei saa x:ää selville millään kohtuullisella vaivalla (kunhan x:kin on niin suuri, että x2 on suurempi kuin n).
Esimerkki: Olkoon p=5 ja q=7, jolloin n=35. Jos x=13, niin y = x2 (mod n) = 169 (mod 35) = 29 (mod 35). Sellaisenaan y (eli kokonaisluku 29) ei ole neliö, mutta kun luvut ovat näin pieniä, löydetään helposti, että modulo 35 se on myös 222, 82 ja 272. (Huomannet, että 13 = −22 modulo 35 ja 27 = −8 modulo 35.)
Tilanne muuttuu, jos joku tuntee p:n ja q:n. Tällöin hän voi laskea erikseen y:n neliöjuuret p:n ja q:n suhteen, sillä alkulukujen suhteen on olemassa tehokkaita algoritmeja tähän tarkoitukseen, toisin kuin siis yhdistetylle luvulle n. Tuloksia on kaksi kummankin alkuluvun suhteen (“plus ja miinus”). Yhdistelemällä saadaan neljä ehdokasta x:ksi. Jos x:ään on koodattu jokin viesti, jossa on mukana hieman redundanssia (esim. luonnollista kieltä tai tarkistussumma), niin viesti erottuu ratkaisujen joukosta. Lievä epäinjektiivisyys (“4-to-1”) ei siis haittaa.
Yleisesti salausavain (edellä “n”) voi siis olla kaikkien saatavilla eli se on julkinen avain. Purkamiseen tarvitaan jokin salausavaimesta riippuva tieto, ns. yksityinen avain (tässä “p ja q”). Se, että nämä avaimet ovat erilaiset, antaa aiheen kutsua julkisen avaimen systeemejä myös epäsymmetrisiksi kryptosysteemeiksi. Joissain tapauksissa, kuten edellä, algoritmikin on hyvin erilainen eri suuntiin. Sitä, että julkisen avaimen laatija tietää, mitä sen takana on (tässä siis tekijöihinjako), sanotaan salaluukuksi (trapdoor). Kaikissa julkisen avaimen systeemeissä on jokin vastaava rakenne. Julkisella avaimella salatun viestin murtajalla on edessään jokin vaikealta näyttävä ongelma, joka ei ole lainkaan hankala, jos vain tuntee salaluukun.
Monessa muussakin järjestelmässä, mm. RSA:ssa, salaluukkuna on julkisen avaimen n tekijöihinjako. Kun n on suuri, sen tekijöiden p ja q löytäminen on hyvin työlästä. Tähän tarvittava tietokoneaika riippuu paitsi n:n suuruudesta ja koneen tehosta myös algoritmista. Nopeimmilla algoritmeilla esim. 1024-bittisen n:n tekijöiden löytäminen kestäisi 107 vuotta koneessa, joka tekee miljoona operaatiota sekunnissa (vrt. kuitenkin Avaimen pituus).
Siispä valittuaan p:n ja q:n satunnaisesti, käyttäjä voi huoletta paljastaa n:n ja antaa toisten lähettää “neliö”viestejä hänelle. Kukaan muu ei niitä saa auki. Tämä on julkisen avaimen kryptografiaa ja luonnosteltu systeemi kantaa Rabinin nimeä (vuodelta 1979). Tämän systeemin murtaminen on yhtäpitävää luvun n tekijöihinjakamisen kanssa (seikka jota ei ole voitu todistaa esim. RSA:sta).
Avaimen kapselointi¶
Julkisen avaimen kryptoalgoritmit operoivat erittäin suurilla luvuilla ja ovat sen vuoksi varsin hitaita. Jos niitä sovellettaisiin koko siihen bittijonoon, jota kulloinkin ollaan salaamassa, laskenta jouduttaisiin toistamaan monta kertaa. Siksi epäsymmetrinen salaus toteutetaan seuraavasti:
Generoidaan avain symmetriselle salausalgoritmille ja salataan data sillä, käyttäen siis nopeaa symmetristä algoritmia kuten AESia. Sen jälkeen salataan avain epäsymmetrisellä algoritmilla. Tätä voisi kutsua digitaaliseksi kirjekuoreksi ja tätä termiä on käytettykin. Nykyinen termi on avaimen kapselointi.
Symmetriset avaimet ovat tyypillisesti enintään muutaman sadan bitin mittaisia, joten epäsymmetrisen algoritmin soveltamista varten tarvitaan bittijonon täyttämistä pidemmäksi (‘padding’). Esimerkiksi RSA:ssa julkisen avaimen moduulin pituus on vähintään 1000 bittiä ja operoitavan luvun pitää olla samanmittainen (mutta moduulia pienempi). Täyttämiseenkin on omat algoritminsa.
Yleisiä julkisen avaimen salausjärjestelmiä (syventävä)¶
Johdannossa esiteltiin jo julkisen ja yksityisen avaimen sekä salaluukun idea käyttäen esimerkkinä Rabinin järjestelmää. Se on sopivan yksinkertainen mutta se ei ole yleisesti käytössä. Samalta aikakaudelta peräisin oleva RSA on tunnetuin epäsymmetrinen kryptosysteemi, tekijöinä Rivest, Shamir ja Adleman, 1978. Salaus muistuttaa Rabinin systeemiä, koska se voisi olla esim. kolmanteen korottamista (Rabinissa neliöintiä). Purkukin on vain yksi potenssiin korotus. Laskut täytyy tietysti tehdä modulo n eli ottaa jakojäännös julkisen moduulin n suhteen. Näin RSA menee:
- selvätekstin x salaus kryptotekstiksi y: y = xe mod n
- Kryptotekstin y purku selvätekstiksi x: x = y d mod n
RSA-avaimet ovat siis
- julkiset: moduuli n ja eksponentti e (encrypt)
- yksityinen: eksponentti d (decrypt)
ja salaluukkuna ovat moduulin tekijät, kaksi suurta alkulukua p ja q. Systeemin muodostaja generoi ja tarkistaa ne, valitsee sitten julkisen e:n (esim. 3 käy) ja laskee siitä yksityisen d:n. Lue seuraava esimerkki, jos haluat tietää miten d lasketaan e:stä.
Esimerkki. Valitaan alkuluvut p=5 ja q=11, jolloin n=55. Olkoon e=3. Siitä saadaan d ratkaisemalla yhtälö e·d=1 mod (p-1)·(q-1) eli 3d=1 mod 40. Tämä onnistuu päässälaskullakin: 3d=41 ei tosin käy, mutta 3d=81 (=9·9) toteutuu kun d=27.
Olkoon viesti m=13. Tällöin kryptoteksti on c=me mod n = 133 mod 55 =2197 mod 55 = 52. Laskimella, jossa tarkkuus riittää, voi heti todeta että cd mod n = 5227 mod 55 = 13. Suoraan korotettuna potenssi on noin 2·1046. On selvää, ettei tällaista operaatiota ehdi eikä mahdu tekemään millään kohtuullisilla resursseilla, kun luvut ovat monisatanumeroisia. Sen vuoksi potenssilasku tehdään seuraavaan tapaan, joka tekee tämän esimerkinkin mahdolliseksi vaikka laskimessa ei olisi kuin vaikkapa kahdeksan numeron tarkkuus.
Esitetään eksponentti kakkosen potenssien summana: 27 = 16+8+2+1, eli binäärilukuna 11011. Tämä tarkoittaa, että
c27=c1· c2· c8· c16 = c· c2· (x2)2· y2, missä on merkitty x= c2 ja y = (x2)2.
Oleellista RSA:n turvallisuuden kannalta on, että julkisista luvuista e ja n ei voi käytännössä laskea yksityistä eksponenttia d. Periaatteessa tämä kävisi jakamalla n ensin tekijöihin p ja q ja ratkaisemalla sitten d kuten laatijakin on tehnyt. Riittäisi tietenkin tuntea tulo (p-1)·(q-1). Ovathan e ja d toistensa käänteislukuja modulo juuri tämä luku.
RSA-systeemin suositeltu avaimenpituus eli moduulin n bittimäärä on aikojen kuluessa kasvanut 512 bitistä 2048 bittiin, toisinaan 3072:een. Paljon lyhyemmillä avaimilla ja samalla nopeammin voidaan toimia, jos käytetään mutkikkaampaa algebraa kuin pelkkiä suuria kokonaislukuja: Nykyään RSA-systeemin osuus jo vähenee ja elliptisten käyrien kryptosysteemit yleistyvät. RSA-systeemiä ei voi toteuttaa elliptisten käyrien aritmetiikassa. Seuraavaksi esiteltävä DHM-avaintenvaihto ja siihen pohjautuva ElGamalin salausjärjestelmä on myös määritelty alun perin samanlaiseen aritmetiikkaan kuin RSA, mutta ne voi toteuttaa elliptisillä käyrillä. Se alkaa olla jo vallitseva tapa.
Toinen erityyppinen algebrallinen struktuuri ovat polynomit, ja niitä hyödyntävä NTRU voi vielä nousta suosituksi. Ainakin se on pärjännyt Post-Quantum Crypto -kisassa.
Diffie-Hellman-Merklen avaintenvaihto¶
Aloitetaan alla olevan videon tarjoamalla numeroesimerkillä. Ilman numeroita ja kaavoja samaan asiaan voi tutustua Computerphilen “vesivärivideolla” tai Wikipedian värikaaviolla.
Salakirjoituksen keskeinen periaate on, että siihen tarvitaan jokin osapuolten tuntema yhteinen salaisuus, avain, jota ei kukaan muu tiedä. Avain on tyypillisesti bittijono, jolla voi olla pituutta esim. 128, ja sen voi yhtä hyvin tulkita kokonaisluvuksi. Avaimesta sopiminen on hankalaa: sitä ei voi lähettää suojattomassa tietoliikennekanavassa eikä sitä toisaalta voi salata, koska ei ole vielä salausavainta.
Nerokas ratkaisu tarjoutuu potenssiin korottamisen laskusäännöistä ja siitä, että logaritmin laskeminen modulaarisessa eli kokonaislukuaritmetiikassa on erittäin vaikeaa, kun luvut ovat suuria. Unohdetaan tässä vaiheessa aritmetiikan modulaarisuus ja keskitytään vain perusideaan:
Kun osapuolet A ja B haluavat generoida yhteisen avaimen, he sopivat kantaluvusta g, jonka ei tarvitse olla salainen. Kumpikin valitsee sitten satunnaisen luvun. Olkoon A:n luku x ja B:n luku y. Kumpikin pitää oman lukunsa salassa, mutta A lähettää B:lle luvun gx ja B lähettää A:lle luvun gy. Yhteisenä avaimena A:lla ja B:llä on nyt luku (gy)x = (gx)y.
Sama asia kaaviona:
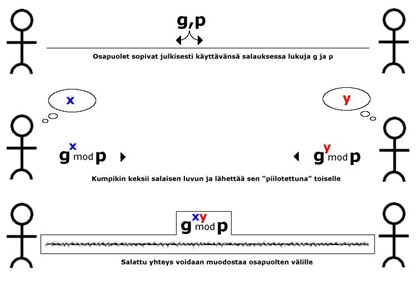
Jotta joku muu saisi selville saman luvun, hänen pitäisi siis luvuista gx ja gy laskea luku gxy. Tätä varten hyökkääjäkin tarvitsisi jommankumman luvuista x ja y, eli hän joutuisi laskemaan logaritmin luvusta gx tai gy. Koska kyseessä on todellisuudessa diskreetti logaritmi kokonaislukuaritmetiikassa (moduulina eli jakajana yhteisesti sovittu suuri eli monisatabittinen alkuluku), ei tämä käy päinsä missään kohtuullisessa ajassa. Diskreetti eksponenttifunktio on yksi kryptografiassa hyödyllisistä yksisuuntaisista funktioista.
Oletetaan, että hyökkääjä C kaappaa A:n ja B:n toisilleen lähettämät viestit (esim. tietoverkon reitittimessä) ja vaihtaa kummankin tilalle luvun gz, missä z on C:n keksimä luku. Nyt A laskee itselleen avaimen gxz ja B avaimen gyz eivätkä ne ole samat. Tämäpä ei haittaa C:tä, sillä C tuntee molemmat nämä avaimet ja pystyy A:n ja B:n “välimiehenä” jatkossa purkamaan A:n viestistä salauksen avaimella gxz ja lähettämään sen edelleen B:lle avaimella gyz salattuna—ja vastaavasti B:ltä A:n suuntaan. Tämän “palvelun” avulla C saa siis selville kaikki luottamukselliseksi tarkoitetut viestit A:n ja B:n välillä ja voi halutessaan tietysti muuttaakin niitä, eivätkä A ja B osaa epäillä mitään.
Tällainen välimies- eli “man-in-the-middle”-hyökkäys pitää ottaa huomioon kaikessa tietoliikenteen turvaamisessa. Yleisesti siinä on kyse tilanteesta, jossa osapuoli C näyttäytyy A:lle B:nä ja B:lle A:na eivätkä nämä pysty edes periaatteessa havaitsemaan asiaa. Tällainen voisi olla mukavaa esimerkiksi, jos pelaa kirjeitse kahta shakin suurmestaria vastaan.
Tässä luonnosteltu Diffie-Hellman-Merklen avaintenvaihtoprotokolla tarvitsee siis lisäksi osapuolten autentikoinnin, jotta C ei pääse väliin. Kun se on hoidossa (ks. esim STS-protokolla), järjestelmä on erittäin hyvä ja se on ollut yksi yleisimmistä rakennuspalikoista tietoturvaprotokollissa. Se on myös ensimmäinen julkaistu julkisen avaimen kryptosysteemi. Vuosi oli 1976, ja julkaisun kirjoittajina olivat Diffie ja Hellman, minkä takia kolmas tekijä on usein jätetty mainitsematta.
Diffie-Hellmanista ElGamaliin (syventävä)¶
Oletetaan, että Diffie-Hellman-Merklen avaintenvaihdon lähtötilanteen eli julkisen lukuparin (g, p) valinnan jälkeen ei ruvetakaan heti vaihtamaan avaimia tai lähettämään viestejä. Sen sijaan kukin osapuoli vain julkaisee oman lukunsa, joka on kantaluku g potenssiin yksityinen ja salainen satunnaisluku (mod p). Jos esimerkiksi A:n yksityinen luku oli x kuten aiemmin, niin A:lla on nyt ikään kuin julkinen avain (X, g, p), missä X = g x mod p. Miten B voi salata viestin m tällä avaimella ja lähettää A:lle, siis suoraan ilman avaintenvaihtoa?
Aloitetaan kuten DHM-avaimenvaihdossa: B luo satunnaisluvun y, joka toimii samoin kuin aiempi B:n luku y. Salatekstin alkuosana B lähettää luvun Y = g y mod p. Jälkiosan pitäisi sitten riippua jotenkin viestistä m (ja varmaan X:stäkin) ja sen pitäisi aueta DHM-tyyppisesti pohjautuen lukuun g xy = Y x mod p, sillä A:han tietää oman yksityisen avaimensa x. Millainen jälkiosa kelpaisi?
Ratkaisu on X y · m mod p ja tuloksena on ElGamalin julkisen avaimen systeemi (vuodelta 1984). Oletuksena on, että salatekstiä satunnaistavalla luvulla y ei ole yhteisiä tekijöitä (p-1):n kanssa. Viestin m purkaminen salatekstistä eli lukuparista (Y, Z) = (g y mod p , X y · m mod p) tapahtuu näin: m = Z / Y x mod p.
Digitaaliset allekirjoitukset¶
RSA:n kehittivät ja sittemmin patentoivat R. Rivest, A. Shamir ja D. Adleman. Alkuperäinen artikkeli vuodelta 1978 on “A method for obtaining digital signatures and public key cryptosystems”. Sama menetelmä toimii molemmissa tarkoituksissa. Sitä vain käytetään allekirjoitukseen toisinpäin kuin salaukseen. Myös useat muut julkisen avaimen salausalgoritmit (erityisesti ElGamal) voidaan muuntaa allekirjoitusalgoritmiksi, mutta niissä eroa on huomattavasti enemmän. Esimerkiksi Rabinin järjestelmässä allekirjoittaminen alkaisi neliöjuurten laskennalla.
Nykyään voi tehdä sähköisiä allekirjoituksia pankkitunnuksilla. Vaikka sellaisten oikeusvaikutus on sama kuin perinteisten—siis paperille käsin kirjoitettujen— allekirjoitusten, kyseessä on käsitteellisesti toisenlainen sähköistys kuin kryptografisesti toteutetussa digitaalisessa allekirjoituksessa. Ero on hyvä pitää mielessä, kun kohtaa allekirjoitustermin eri yhteyksissä.
Kryptografinen allekirjoitus on periaatteessa hyvin yksinkertainen operaatio. Allekirjoittaja laskee viestistä tai dokumentista matemaattisen funktion yksityisellä avaimella, jota kukaan muu ei tiedä. Kuka tahansa muu voi todentaa allekirjoituksen tuohon yksityiseen avaimeen matemaattisesti liittyvällä julkisella avaimella. Funktion ominaisuuksien takia allekirjoituksen väärentäminen on laskennallisesti mahdotonta. Muut eivät siis voi luoda uusia allekirjoituksia eri viesteille tai huomaamatta muuttaa jo allekirjoitettua dokumenttia toiseksi.
Pankkitunnuksilla allekirjoittaminen tuottaa kyllä lain vaatiman aitouden. Toisin sanoen allekirjoittaja, eikä kukaan muu, on tarkoituksellisesti laatinut kyseisen allekirjoituksen juuri kyseiseen dokumenttiin tai viestiin. Kaiken allekirjoittamiseen vaadittavan datan on kuitenkin pankki toimittanut asiakkaalleen. Matemaattisen rakenteen sijasta tässä tarvitaan luottamusta ja se on osoittautunut riittäväksi. Digitaaliset allekirjoitukset esimerkiksi henkilökortin kansalaisvarmenteeseen kuuluvilla yksityisillä avaimilla eivät ole yleistyneet samassa määrin kuin pankkien tarjoamat allekirjoituspalvelut. Muitakin palveluita on rakennettu, ja kryptografinen allekirjoitus on kyllä voimissaan kaikissa näissä järjestelmissä, myös siis pankkitunnuksilla allekirjoittamisessa. Sen asema vain on tekninen eikä sellainen, että henkilö hallinnoisi ja tietoisesti käyttäisi omaa yksityistä avaintaan. Sen sijaan henkilön hallussa oleva laite autentikoituu digitaalisen allekirjoituksen tekniikalla palveluntarjoajan järjestelmään, jossa henkilön tunnistautuminen jatkuu ja johtaa varmuuteen myös allekirjoitusten oikeellisuudesta.
On vasta puolet totuudesta, kun edellä sanottiin, että kryptografinen allekirjoitus on yksinkertaista. Matemaattisen osuuden lisäksi tarvitaan julkisten avainten hallintaa osoittamaan pitävästi, mikä julkinen avain vastaa kenenkin yksityistä avainta. Tästä päädytään periaatteessa samantapaisiin luottamusrakenteisiin kuin edellä käsitellyt pankkien ja muiden järjestelmät. Jo mainittuun kansalaisvarmenteeseen, samoin kuin teleoperaattoreiden tarjoamaan mobiilivarmenteeseen, liittyy juuri tällaisia rakenteita. Niistä käytetään termiä PKI, public key infrastructure.
Miten siis aito digitaalinen allekirjoitus muodostetaan ja todennetaan RSA-järjestelmässä? Julkisen RSA-avaimen (n,e) luoja, sanokaamme Liisa, tuntee yksityisen eksponentin d [(syventävästi) = se luku, jonka Liisa laski yhtälöstä e·d=1 modulo (p-1)·(q-1) generoituaan suuret alkuluvut p ja q]. Liisa voi nyt laskea viestistä m potenssin s=md mod n. Kun Liisa lähettää tai tallentaa luvut m ja s Pekalle, tämä voi tarkistaa, että m = se mod n, olettaen että hän tuntee julkiset luvut n ja e. Jos yhtälö pätee, Liisa ei voi kiistää allekirjoittaneensa viestiä m—paitsi väittämällä että hänen avaimensa on paljastunut.
Menemättä nyt PKI-rakenteisiin huomautetaan vain, että RSA-systeemissä ei itse asiassa tarvitse lähettää viestiä m lainkaan, sillä sehän ratkeaa kun allekirjoitus s korotetaan potenssiin e mod n. Jos saadusta yli 1000-bittisestä luvusta dekoodautuu jokin luonnollisen kielen teksti, tässä ei ole mitään ongelmaa: se on allekirjoitettu viesti. Pariin tuhanteenkaan bittiin ei mahdu kovin paljon tekstiä allekirjoitettavaksi. Sen vuoksi epäsymmetrisen systeemin allekirjoituskäytössä sovelletaan vastaavaa ideaa kuin salauksessa, jossa kapseloidaan symmetrinen avain. Allekirjoituksessa “kapseloidaan” viestin tiiviste. Toisin sanoen, viestistä m, olipa se kuinka pitkä tahansa, lasketaan kryptografinen tiiviste H(m), josta lasketaan allekirjoitus s. Vastaanottajalle lähetetään m ja s. RSA:n tapauksessa viestinä on siis m ja (H(m))d mod n. Kuten avaimen kapseloinnissa myös tässä tarvitaan täyttöä, eli H(m):n pari sataa bittiä täytetään moduulin n mittaiseksi.
Digitaaliset allekirjoitukset TLS:sä
PKI:sta on oma lukunsa myöhempänä materiaalissa, joten kovin syvällisesti siihen ei tässä esimerkissä kannata mennä. TLS käyttää epäsymmetristä salausta (symmetristen) avainten vaihtoon sekä osapuolten autentikointiin. Toisin sanoen siihen, että osapuolet voivat olla varmoja siitä, että toinen osapuoli on oikeasti se, kuka hän väittää olevansa. Yleensä riittää, että palvelin autentikoi itsensä asiakkaalle. Esimerkiksi Facebookin ei tarvitse saada identiteetistäsi varmuutta (ainakaan epäsymmetrisen salauksen turvin), mutta sinä haluat olla varma siitä, että facebook.com on edelleen Meta-yrityksen hallussa. Ilman autentikointia vaarana olisi se, että mikäli Meta unohtaisi uusia sopimuksen facebook.com-URL:n omistuksesta, voisi hyökkääjä ostaa sen itselleen. Käyttäjälle tämä muutos ei välttämättä pelkän etusivun perusteella näkyisi, olettaen, että hyökkääjä tekisi etusivusta riittävän uskottavan näköisen. Autentikoinnin kanssa selaimesi puolestaan ilmoittaisi muuttuneesta/puuttuvasta varmenteesta, ja estäisi pääsyn sivulle.
Edellisestä esimerkistä muistanet, että symmetrisen salauksen virkaa esitti Teijan ja Teemun yhteinen tallelokero. Avain pitäisi nyt saada molemmille, mutta syystä x he eivät voi hoitaa avaintenvaihtoa kasvotusten. Niinpä se tehdään kirjeitse, joka on esimerkissämme epäsymmetrisen salauksen vertauskuva. Teijalla on avaimet hallussaan, mutta lähettääkseen toisen Teemulle hän haluaa varmuuden siitä, että Teemu todellakin on se, joka hän väittää olevansa. Siispä hän pyytää Teemua lähettämään hänelle kirjekuoren, johon Teemu on hakenut Poliisin allekirjoituksen. Jotta esimerkki toimisi hieman paremmin, joudumme käyttämään hieman mielikuvitusta:
- Teemulla on kirjekuori (julkinen avain), jonka saa sulkemisen jälkeen auki vain Teemun omalla kirjeveitsellä (yksityinen avain).
- Teemu menee poliisiasemalle, jossa hän todistaa henkilöllisyytensä, ja pyytää Poliisin allekirjoitusta kirjekuoreen.
- Poliisin allekirjoituksen saatuaan Teemu lähettää avoimen kirjekuorensa Teijalle.
- Teija näkee Poliisin allekirjoituksesta että kirjekuori on Teemun, ja pistää toisen avaimista kirjekuoreen. Kuoren suljettuaan hän ei saa sitä enää auki.
- Teija lähettää kirjeen Teemulle, joka saa kuoren auki veitsellään.
Tämä oli siis hieman lennokas esimerkki TLS-kättelystä, josta voit halutessasi lukea lisää täältä. Poliisi toimitti esimerkissä Certificate Authorityn virkaa, josta voit lukea lisää täältä. Tämän sivun ensimmäiseen esimerkkiin taas pääset tästä
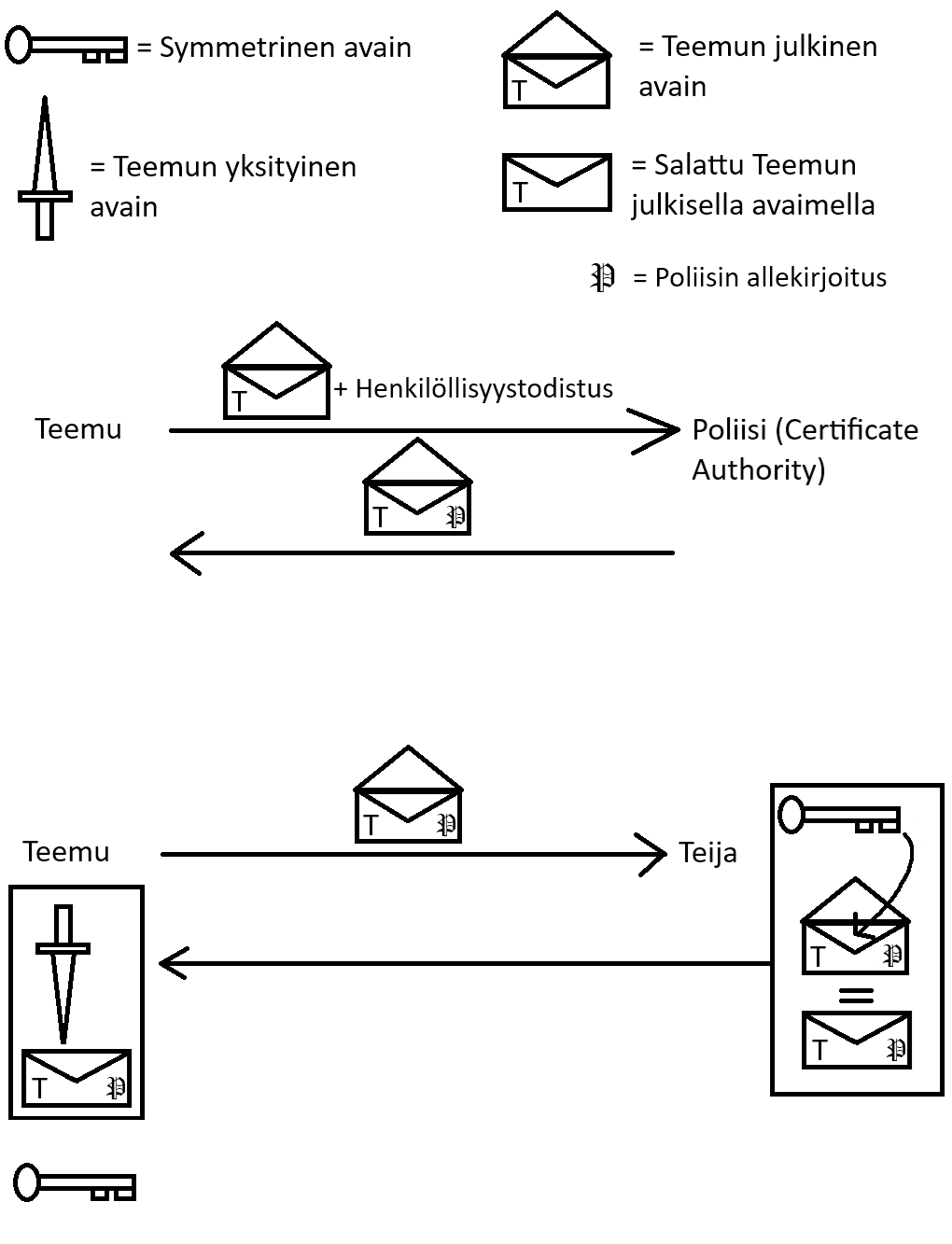
Kuva havainnollistaa yllä esitettyä tapahtumaketjua. Huomaa, että oikeassa TLS-kättelyssä allekirjoitusta ei haeta joka kerralla erikseen Certificate Authorityltä.
Kryptografian monimuotoisuus¶
Tähänastinen sovelletun kryptografian pääluku on keskittynyt tärkeimpiin algoritmeihin ja skeemoihin, joita kohdataan nykyään käytössä olevissa järjestelmissä. Alla oleva käsitekartta tuo näkyviin myös protokollat, joita käsitellään tuonnempana. Värien tarkoitus on kytkeä erilaisia käyttötapoja algoritmien nimiin ja tyyppeihin.
Matemaattinen tutkimus yhdessä systeemiajattelun kanssa tuo ja parantaa jatkuvasti uusia lähestymistapoja, jotka tekevät kryptografian soveltuvaksi uusiin tilanteisiin. Lohkoketjut mainittiin tiivistefunktioita jäsentävässä kartassa. Alla olevassa kartassa homomorfinen salaus tarkoittaa “laskentakelpoisia kryptotekstejä”. Tietysti aina voi summata tai kertoa kaksi salattua bittijonoa keskenään, mutta tuloksen salausta purettaessa tuskin tulee mitään järkevää – puhumattakaan että siinä olisi selvätekstien summa tai tulo. Haasteena on pitää kryptotekstin rakenne laskentakelpoisena mutta kryptoanalyytikon ulottumattomissa.
Järjestelmäkehittäjillä on monia ideoita otettavaksi käyttöön heti, kun täysin homomorfiset salausjärjestelmät yleistyvät. Sama pätee identiteettipohjaiseen salaukseen, jossa “olet avaimesi”, ja moniin muihin kryptografisiin kehitelmiin. Vilkaisu kirjallisuuteen paljastaa, että tässä kartassa on vain jäävuoren huippu suhteessa siihen, minkä verran kryptografisia ideoita on tutkittu. Suurinta osaa toimivistakaan ideoista ei ole standardoitu tai niillä ei ole helposti saatavilla olevia tuotantolaadun toteutuksia tai ne eivät ole täysin valmiita niin, että ohjelmistosuunnittelija voisi helposti toteuttaa ne. On pitkä tie kryptografiasta sellaisena kuin se esitetään useimmissa tutkimusartikkeleissa kryptografiaan sellaisena kuin sen pitää olla käyttöönottoa varten.
Vaikka et syventyisi matemaattiseen tutkimukseen, voit menestyä suunnittelemalla ennennäkemättömiä järjestelmiä, jotka perustuvat tutkijoiden todistamiin turvaominaisuuksiin. Tämän pitäisi toimia motivaationa opiskella ei-viihdyttäviä perusteita kunnolla. Vähemmänkin innovatiivisissa opiskelutavoitteissa perusteiden motivaatio on juuri siinä, mitä kartta yrittää opettaa: pääkäsitteiden järjestämisessä mielekkäällä tavalla.
Huomautus käsitekartan saavutettavuudesta.
Hyökkääjän ominaisuuksiin varautuminen¶
Tässä tekstissä kryptografian käyttäjän vastustaja on jäänyt kovin abstraktiksi eikä kaikissa kohdin ole edes käsitelty murtamisen mahdollisuuksia. Kryptografian teoria mallintaa hyökkääjää esimerkiksi sen mukaan, mitä hän tietää: pelkän kryptotekstin, tunnetun selvätekstin, valitun selvätekstin, adaptiivisesti valitun selvätekstin, tai valitun kryptotekstin. Näillä skenaarioilla on lyhenteet COA, KPA, CPA, CPA2, CCA ja lisäksi jopa CCA2, missä A tarkoittaa Attack, K=known, P=plaintext, C=cryptotext ja chosen, 2=adaptive ja O=only. Sitten voidaan tarkastella, minkä verran hyökkääjä voi saada selville salatusta selvätekstistä (tai CCA-tapauksessa avaimesta) tietyillä määrillä resursseja. Allekirjoituksiin ja MAC-koodeihin on omat skenaarionsa. Tiettyihin tarkoituksiin pitää käyttää vähintään tietyn tasoisen hyökkääjän kestäviä primitiivejä.
Käytännössä hyökkääjillä on erilaisia motiiveja ja taitotasoja ja heidän käytössään on vaihtelevan tasoiset laskennalliset resurssit. Yleensä halutaan suunnitella kryptografisia komponentteja, joita voidaan käyttää useissa erilaisissa sovelluksissa. Sen vuoksi täytyy olla konservatiivisia hyökkääjän mallintamisessa, olettaen ainakin, että se pystyy hyödyntämään merkittävän määrän resursseja.
Käytännön järjestelmissä ei pystytä saavuttamaan ehdotonta turvallisuutta, joka suojaisi rajoittamatonta laskentatehoa vastaan. Tällaiset järjestelmät kuluttaisivat suuria määriä avainmateriaalia, jota ei voida luoda julkisen avaimen menetelmillä (vaan se pitäisi kuljettaa erikseen kuten kerta-avainjärjestelmässä). Tämän vuoksi asetetaan rajoituksia mallinnettavan hyökkääjän laskennallisille kyvyille. Tyypillinen tavoite on edellyttää hyökkääjältä työmäärä, joka on verrattavissa lohkosalaimen, kuten AES:n, 128-bittisen avaimen tyhjentävään hakuun eli raa’an voiman murtamiseen. Tällaisessa tapauksessa puhutaan 128-bittisestä suojaustasosta. Tällainen laskennallinen saavutus näyttää edelleen olevan jopa valtiollisten turvallisuusvirastojen horisontin ulkopuolella. Niiden kykyjä on vaikea arvioida, mutta vertailun vuoksi globaalissa Bitcoin-louhinnassa suoritettavien hash-laskelmien määrä on tällä hetkellä noin 267 kpl sekunnissa ja sen sähkönkulutus on pienen valtion tasolla. Tällä nopeudella ja olettaen, että hash-laskun kustannukset ovat samat kuin AES-avaimen testaamisen, tyhjentävä avaimen haku vaatisi silti 236 eli noin 1011 vuotta. Jos ollaan vielä varovaisempia tai halutaan erittäin suuri suojausmarginaali pitkällä aikavälillä (jonka aikana isoja kvanttitietokoneita saattaa tulla saataville) tai huolena ovat useaan kohteeseen suunnatut hyökkäykset, 192- tai 256-bittisen suojauksen tavoittelu voi tuntua houkuttelevalta.
Varovaisuus vaatii myös torjumaan algoritmeja ja järjestelmiä, joissa on tunnettuja heikkouksia, vaikka ne näyttävät vähäisiltä. Kryptoanalyyttiset hyökkäykset vain vahvistuvat ajan myötä, joko laskennan kehityksen tai uusien kryptoanalyyttisten ideoiden kehittämisen vuoksi. Tällainen varovaisuus tuottaa ristiriidan sen tosiasian kanssa, että yhden kryptojärjestelmän korvaaminen toisella voi olla kallista ja aikaa vievää, ellei järjestelmään ole sisäänrakennettu ketteryyttä. Tietojärjestelmät ovat usein täynnä vanhoja salausjärjestelmiä, joiden päivitys on hankalaa tai ei kiinnosta omistajia, ennen kuin käytännön murtuminen on tapahtunut.
Formaalien määritelmien ja todistusten merkitys (syventävä)¶
Kryptografisten järjestelmien turvallisuusanalyysi on saavuttanut kypsyysasteen, jossa ei pitäisi koskaan olla tarvetta ottaa käyttöön kryptografista skeemaa tai protokollaa, jolla ei olisi selkeää syntaksia ja täsmällistä turvallisuustodistusta selkeästi ilmaistujen oletusten mukaisesti. Valitettavasti tämä sääntö jää edelleen usein huomiotta käytännössä. Tämä jättää tutkijoille mahdollisuuden jälkikäteisiin analyyseihin, joissa joko löydetään vikoja tai tuotetaan myönteisiä tuloksia. Ihanteellisessa maailmassa ensin kerättäisiin kaikki vaatimukset uudelle skeemalle tai protokollalle, sitten suunnitellaan järjestelmä ja samanaikaisesti kehitetään sille turvallisuustodistuksia. Todellisuudessa ollaan usein suunnittelu–julkaisu–murto–korjaus -syklin loukussa. Välimuotoa suunnittelu–murto–korjaus–julkaisu käytettiin TLS-protokolla versiossa 1.3.
Avaimen pituus (syventävä)¶
Edellä on jo tullut esille, miksi 128-bittiseen suojaustasoon pyrkiminen on järkevää: se tarjoaa riittävän suojausmarginaalin lähes kaikissa tavanomaisen tietojenkäsittelyn tilanteissa. Toinen syy on se, että tiettyjä sovellusalueita, kuten rajoitettuja laskentaympäristöjä, lukuun ottamatta, se on tehokkaasti saavutettavissa. Toisin sanoen ei ole mitään hyvää syytä olla pyrkimättä näin korkealle.
Algoritmeilla ja niiden avaimilla on rajallinen elinikä. Kryptoanalyysin edistyminen voi tehdä aiemmista turvallisista algoritmeista tai avainten pituuksista turvattomia. Lisäksi mitä kauemmin sama avain on käytössä, sitä todennäköisemmin se vaarantuu. Avaimen elinkaareen liittyviä asioita käsitellään tarkemmin avaintenhallinnan yhteydessä. Algoritmien ja avainten koon muuttaminen voi olla hankalaa ja kallista. Tämä antaa perusteita varovaisten valintojen tekemiseksi jo järjestelmien alkuvaiheessa.
Tavoitteena oleva 128 bitin suojaustaso nostaa kutenkin tehokkuusnäkökohdat esille, erityisesti epäsymmetrisissä algoritmeissa. Esimerkiksi on arvioitu, että 2128:n vaivaa vastaavan suoran tekijöihinjakohyökkäyksen torjuminen vaatisi 3072-bittisen RSA-moduulin käyttöä. Tämä johtuu tunnetuimman tekijöihinjakoalgoritmin (number field sieve) subeksponentiaalisesta kompleksisuudesta. Näin suuri moduuli hidastaa merkittävästi RSA:n perusoperaatioita (työmäärä kasvaa yleensä kuutiollisesti suhteessa moduulin bittimäärään). Sama pätee diskreetin logaritmin vaikeuteen perustuviin järjestelmiin (esim. Diffie-Hellman-Merkle ja ElGamal), silloin kun ne käyttävät modulaarista aritmetiikkaa. Elliptisillä käyrillä laskettava diskreetti logaritmi ei ole nopeutettavissa vastaavalla tavalla. Sen ansiosta voidaan käyttää paljon pienempiä parametreja: 128-bittisen suojaustason toteuttamiseen riittää elliptinen käyrä 256-bittisessä kerroinkunnassa. Toisin sanoen 128 bitin turvallisuus saavutetaan elliptispohjaisissa järjestelmissä tehokkaammin kuin perinteisissä. Kontrasti on vielä jyrkempi, jos tähdätään 256-bittiselle suojaustasolle: siellä NIST suosittelee 15360-bittisiä julkisia RSA-avaimia, kun taas elliptiseltä kryptolta vaadittu avaimen koko kasvaa vain 512 bittiin.
Kryptografinen ketteryys (syventävä)¶
Toisinaan jossain järjestelmässä tai protokollassa on tarpeen vaihtaa algoritmi toiseen saman tyyppiseen. Yksi syy voi olla se, että alkuperäinen algoritmi on murtunut. Tiivistefunktiot tarjoavat merkittävän esimerkin, sillä aikoinaan turvallisia hash-funktioita, kuten MD5:ä, pidetään nykyään täysin turvattomina. Toinen syy voi olla, että saatavilla on tehokkaampi vaihtoehto, esimerkiksi elliptiset käyrät RSA:n tilalle. Kolmas syy on varautuminen teknologian muutokseen – esimerkkinä siirtyminen post-quantum -kryptoon suojaksi suurten kvanttitietokoneiden kehitykseltä.
Vaihtoa helpottaa, jos järjestelmä tai protokolla on kryptografisesti ketterä – eli jos siinä on sisäänrakennettu kyky vaihtaa algoritmi toiseen tai versiosta toiseen. Tämä ominaisuus on käytössä protokollissa IPsec, SSH ja TLS, joiden alussa tehdään neuvottelu salauspaketista (cipher suite) ja protokollan versiosta. Tällaisen toiminnon lisääminen jo ennestään monimutkaiseen protokollaan voi aiheuttaa haavoittuvuuden, koska itse neuvottelumekanismeista voi tulla heikkous. Esimerkki tästä ovat SSL/TLS:n yhteydessä tehdyt downgrade-hyökkäykset, jotka ovat hyödyntäneet eri protokollaversioiden rinnakkaiseloa sekä protokollissa ollutta tukea tarkoituksellisesti heikennetyille (USA:n vientikieltoa noudattaneille) “EXPORT”-salausohjelmistoille. Kryptografinen ketteryys voi myös aiheuttaa ohjelmiston paisumista, koska on houkuttelevaa lisätä siihen kaikkien toiveiden mukaiset algoritmit.
Ketterän krypton vastakohtana ovat järjestelmät (ja niiden suunnittelijat), jotka rajoittavat krypton yhteen joukkoon algoritmeja. VPN-protokolla nimeltä WireGuard on esimerkki tästä. Siinä ei voi muuttaa algoritmeja eikä protokollan versiokenttää.
On tietysti olemassa keskitie: tuetaan kryptografista ketteryyttä mahdollisuuksien mukaan, mutta hallitaan tiukasti, mitä algoritmeja ja vanhoja versioita tuetaan.
Standardoidun kryptografian kehittäminen (syventävä)¶
Bittien kryptografinen käsittely kannattaa standardoida, jotta kommunikointi käy mahdolliseksi. Standardeja laaditaan monella tasolla ja taholla: kansainvälisesti, alueellisesti ja tiettyjen teollisuusryhmittymien puitteissa. Jotkin keskeiset asiat saavat standardin statuksen usean tahon toimesta. Esimerkiksi RSA on standardi ISO/IEC 9796, IEEE Std 1363-2000, ANSI X9.31 ja PKCS#1. Nämä ovat eri-ikäisiä versioita ytimeltään samasta asiasta. Eroja on parametrien valinnassa ja perusalgoritmin ympärille rakennetuissa skeemoissa.
Tietoverkkojen kannalta tärkeitä ovat IETF:n Internet-standardit, eli RFC:t (“Request of comments”). Monet niistä ovat muiden standardien kopioita tai kehittyneempiä versioita, esim. Netscape-yrityksen julkaisemasta SSL3.0:sta tuli TLS: ensin RFC2246, sitten versiot 1.1, 1.2 ja 1.3 RFC-numeroissa 4346, 5246 ja 8446 (1999-2006-2008-2018).
Kryptografian kannalta tärkeimmät standardointiorganisaatiot ovat jo mainitut kansainväliset ISO/IEC ja IETF sekä Yhdysvaltain NIST. Näiden työskentelytavat poikkeavat toisistaan. ISO/IEC toimii suljetuimmin, NIST järjestää avoimia kommenttikierroksia ja toisinaan kryptokilpailuja (kuten AESia varten tehtiin), ja IETF:ään voi kuka tahansa liittyä.
Standardointielimet eivät ole täydellisiä. Liian monet tekijät ja tuotokset voivat johtaa kryptografian hajaantumiseen, mikä vaikeuttaa yhteentoimivuuden saavuttamista. Voi myös syntyä hienoista yhteensopimattomuutta algoritmien eri versioiden välillä. Jopa täysin avoimet standardointielimet eivät välttämättä pysty keräämään palautetta oikeilta sidosryhmiltä. Standardoiduksi voi myös tulla ennenaikaisesti versio, joka myöhemmin havaitaan jollain tavoin puutteelliseksi tai jossa parannetut vaihtoehdot tulevat esiin vasta myöhemmin. Kun standardi on asetettu, eikä vakavia hyökkäyksiä ole ilmennyt, voi puuttua intoa parantaa sitä. RSA:han perustuvien salausjärjestelmien historia havainnollistaa näitä ilmiöitä hyvin. Erityisesti sen parhaat avaimen kapselointimenettelyt eivät ole yleistyneet.
Standardointielimet voivat olla alttiita sille, että tiettyjä kansallisia tai kaupallisia etuja edustavat ryhmät voivat vaikuttaa niiden työhön. Esimerkiksi Yhdysvaltain NSA:lla oli aikoinaan rooli DES-algoritmin suunnittelussa, ja sittemmin se suoritti näennäissatunnaisbittien generaattorin yleissuunnittelun ja tiettyjen kriittisten parametrien valinnan NIST-standardia varten (ks. Dual_EC_DBRG esim. Wikipediasta). Tällaisissa yhteyksissä on keskeistä, että kaikkien kansallisten tai kaupallisten sidosryhmien rooli on läpinäkyvä. Esimerkiksi NIST on tarkistanut kryptografian standardointiprosessiaan lisätäkseen avoimuutta ja vähentääkseen riippuvuutta ulkoisista organisaatioista.