1. MATH.APP.210
  2. 3. Odotusarvo
  3. 3.1 Odotusarvo, varianssi ja keskihajonta ja fraktiilit
\[\newcommand{\N}{\mathbb N} \newcommand{\Z}{\mathbb Z} \newcommand{\Q}{\mathbb Q} \newcommand{\R}{\mathbb R} \newcommand{\C}{\mathbb C} \newcommand{\ba}{\mathbf{a}} \newcommand{\bb}{\mathbf{b}} \newcommand{\bc}{\mathbf{c}} \newcommand{\bd}{\mathbf{d}} \newcommand{\be}{\mathbf{e}} \newcommand{\bff}{\mathbf{f}} \newcommand{\bh}{\mathbf{h}} \newcommand{\bi}{\mathbf{i}} \newcommand{\bj}{\mathbf{j}} \newcommand{\bk}{\mathbf{k}} \newcommand{\bN}{\mathbf{N}} \newcommand{\bn}{\mathbf{n}} \newcommand{\bo}{\mathbf{0}} \newcommand{\bp}{\mathbf{p}} \newcommand{\bq}{\mathbf{q}} \newcommand{\br}{\mathbf{r}} \newcommand{\bs}{\mathbf{s}} \newcommand{\bT}{\mathbf{T}} \newcommand{\bu}{\mathbf{u}} \newcommand{\bv}{\mathbf{v}} \newcommand{\bw}{\mathbf{w}} \newcommand{\bx}{\mathbf{x}} \newcommand{\by}{\mathbf{y}} \newcommand{\bz}{\mathbf{z}} \newcommand{\bzero}{\mathbf{0}} \newcommand{\nv}{\mathbf{0}} \newcommand{\cA}{\mathcal{A}} \newcommand{\cB}{\mathcal{B}} \newcommand{\cC}{\mathcal{C}} \newcommand{\cD}{\mathcal{D}} \newcommand{\cE}{\mathcal{E}} \newcommand{\cF}{\mathcal{F}} \newcommand{\cG}{\mathcal{G}} \newcommand{\cH}{\mathcal{H}} \newcommand{\cI}{\mathcal{I}} \newcommand{\cJ}{\mathcal{J}} \newcommand{\cK}{\mathcal{K}} \newcommand{\cL}{\mathcal{L}} \newcommand{\cM}{\mathcal{M}} \newcommand{\cN}{\mathcal{N}} \newcommand{\cO}{\mathcal{O}} \newcommand{\cP}{\mathcal{P}} \newcommand{\cQ}{\mathcal{Q}} \newcommand{\cR}{\mathcal{R}} \newcommand{\cS}{\mathcal{S}} \newcommand{\cT}{\mathcal{T}} \newcommand{\cU}{\mathcal{U}} \newcommand{\cV}{\mathcal{V}} \newcommand{\cW}{\mathcal{W}} \newcommand{\cX}{\mathcal{X}} \newcommand{\cY}{\mathcal{Y}} \newcommand{\cZ}{\mathcal{Z}} \newcommand{\rA}{\mathrm{A}} \newcommand{\rB}{\mathrm{B}} \newcommand{\rC}{\mathrm{C}} \newcommand{\rD}{\mathrm{D}} \newcommand{\rE}{\mathrm{E}} \newcommand{\rF}{\mathrm{F}} \newcommand{\rG}{\mathrm{G}} \newcommand{\rH}{\mathrm{H}} \newcommand{\rI}{\mathrm{I}} \newcommand{\rJ}{\mathrm{J}} \newcommand{\rK}{\mathrm{K}} \newcommand{\rL}{\mathrm{L}} \newcommand{\rM}{\mathrm{M}} \newcommand{\rN}{\mathrm{N}} \newcommand{\rO}{\mathrm{O}} \newcommand{\rP}{\mathrm{P}} \newcommand{\rQ}{\mathrm{Q}} \newcommand{\rR}{\mathrm{R}} \newcommand{\rS}{\mathrm{S}} \newcommand{\rT}{\mathrm{T}} \newcommand{\rU}{\mathrm{U}} \newcommand{\rV}{\mathrm{V}} \newcommand{\rW}{\mathrm{W}} \newcommand{\rX}{\mathrm{X}} \newcommand{\rY}{\mathrm{Y}} \newcommand{\rZ}{\mathrm{Z}} \newcommand{\pv}{\overline} \newcommand{\iu}{\mathrm{i}} \newcommand{\ju}{\mathrm{j}} \newcommand{\im}{\mathrm{i}} \newcommand{\e}{\mathrm{e}} \newcommand{\real}{\operatorname{Re}} \newcommand{\imag}{\operatorname{Im}} \newcommand{\Arg}{\operatorname{Arg}} \newcommand{\Ln}{\operatorname{Ln}} \DeclareMathOperator*{\res}{res} \newcommand{\re}{\operatorname{Re}} \newcommand{\im}{\operatorname{Im}} \newcommand{\arsinh}{\operatorname{ar\,sinh}} \newcommand{\arcosh}{\operatorname{ar\,cosh}} \newcommand{\artanh}{\operatorname{ar\,tanh}} \newcommand{\sgn}{\operatorname{sgn}} \newcommand{\diag}{\operatorname{diag}} \newcommand{\proj}{\operatorname{proj}} \newcommand{\rref}{\operatorname{rref}} \newcommand{\rank}{\operatorname{rank}} \newcommand{\Span}{\operatorname{span}} \newcommand{\vir}{\operatorname{span}} \renewcommand{\dim}{\operatorname{dim}} \newcommand{\alg}{\operatorname{alg}} \newcommand{\geom}{\operatorname{geom}} \newcommand{\id}{\operatorname{id}} \newcommand{\norm}[1]{\lVert #1 \rVert} \newcommand{\tp}[1]{#1^{\top}} \renewcommand{\d}{\mathrm{d}} \newcommand{\sij}[2]{\bigg/_{\mspace{-15mu}#1}^{\,#2}} \newcommand{\abs}[1]{\lvert#1\rvert} \newcommand{\pysty}[1]{\left[\begin{array}{@{}r@{}}#1\end{array}\right]} \newcommand{\piste}{\cdot} \newcommand{\qedhere}{} \newcommand{\taumatrix}[1]{\left[\!\!#1\!\!\right]} \newenvironment{augmatrix}[1]{\left[\begin{array}{#1}}{\end{array}\right]} \newenvironment{vaugmatrix}[1]{\left|\begin{array}{#1}}{\end{array}\right|} \newcommand{\trans}{\mathrm{T}} \newcommand{\EUR}{\text{\unicode{0x20AC}}} \newcommand{\SI}[3][]{#2\,\mathrm{#3}} \newcommand{\si}[2][]{\mathrm{#2}} \newcommand{\num}[2][]{#2} \newcommand{\ang}[2][]{#2^{\circ}} \newcommand{\meter}{m} \newcommand{\metre}{\meter} \newcommand{\kilo}{k} \newcommand{\kilogram}{kg} \newcommand{\gram}{g} \newcommand{\squared}{^2} \newcommand{\cubed}{^3} \newcommand{\minute}{min} \newcommand{\hour}{h} \newcommand{\second}{s} \newcommand{\degreeCelsius}{^{\circ}C} \newcommand{\per}{/} \newcommand{\centi}{c} \newcommand{\milli}{m} \newcommand{\deci}{d} \newcommand{\percent}{\%} \newcommand{\Var}{\operatorname{Var}} \newcommand{\Cov}{\operatorname{Cov}} \newcommand{\Corr}{\operatorname{Corr}} \newcommand{\Tasd}{\operatorname{Tasd}} \newcommand{\Ber}{\operatorname{Ber}} \newcommand{\Bin}{\operatorname{Bin}} \newcommand{\Geom}{\operatorname{Geom}} \newcommand{\Poi}{\operatorname{Poi}} \newcommand{\Hyperg}{\operatorname{Hyperg}} \newcommand{\Tas}{\operatorname{Tas}} \newcommand{\Exp}{\operatorname{Exp}} \newcommand{\tdist}{\operatorname{t}} \newcommand{\rd}{\mathrm{d}}\]

Odotusarvo, varianssi ja keskihajonta ja fraktiilit

Satunnaismuuttujien todennäköisyysjakaumia voidaan luonnehtia erilaisin tunnusluvuin. Pelkästään jakauman tyypin ja sen tunnuslukujen avulla voidaan tehdä hyödyllisiä johtopäätöksiä tarkasteltavasta satunnaiskokeesta. Tavallisimmat jakauman sijaintia kuvaavat tunnusluvut ovat odotusarvo, varianssi ja keskihajonta sekä erilaiset fraktiilit. Odotusarvo ja fraktiileista mediaani ilmoittavat jakauman keskikohdan, kun taas varianssi ja keskihajonta mittaavat jakauman hajaantumisen suuruutta.

Diskreetit satunnaismuuttujat

Määritelmä 3.1.1

Diskreetin satunnaismuuttujan \(X\), jonka otosavaruus on \(\Omega\) ja tiheysfunktio \(f(x)\), odotusarvo (mean, expected value) \(\rE(X)\), varianssi (variance) \(\Var(X)\) ja keskihajonta (standard deviation) \(\rD(X)\) ovat

\[\begin{split}\begin{aligned} \rE(X) &= \mu = \sum_{x \in \Omega} xf(x), \\ \Var(X) &= \sigma^2 = \sum_{x \in \Omega} (x - \mu)^2f(x), \\ \rD(X) &= \sigma = \sqrt{\Var(X)}. \end{aligned}\end{split}\]

Heitetään harhatonta, eli kaikille tulosvaihtoehdoille tasapuolista kolikkoa kolme kertaa.

Mikä on kruunien lukumäärän odotusarvo heittosarjassa?
Mikä on kruunien lukumäärän varianssi heittosarjassa?

Huomautus 3.1.2

Jos otosavaruudessa on ääretön määrä alkioita, on tunnusluku olemassa vain, kun sen määrittelevä sarja suppenee ja summa on termien järjestyksestä riippumaton. Diskreetin muuttujan odotusarvo on mahdollisten arvojen \(x\) todennäköisyyksillään \(P(X=x)=f(x)\) painotettu keskiarvo. Varianssi taas on odotusarvosta laskettujen neliöityjen poikkeamien \((x-\mu)^2\) todennäköisyyksillä painotettu keskiarvo.

Fysikaalisesta näkökulmasta satunnaismuuttujan odotusarvolla ja varianssilla on seuraavanlaiset tulkinnat. Jos ajatellaan, että yhden yksikön verran “todennäköisyysmassaa” on jaettu otosavaruuden \(\Omega\) pisteisiin \(x\) lukusuoralla pistetodennäköisyyden \(f(x)\) verran, niin odotusarvo ilmoittaa kyseisen lukusuoran massakeskipisteen ja varianssi sen hitausmomentin massakeskipisteakselin suhteen.

Esimerkki 3.1.3

Arpanopan silmäluvun \(X\sim\mathrm{Tasd}(1,6)\) tiheysfunktio on \(f(x) = \frac{1}{6}\) ja otosavaruus \(\Omega=\{1,2,3,4,5,6\}\). Määritelmän mukaan odotusarvo ja varianssi ovat

\[\begin{split}\begin{aligned} \rE(X) &= \sum_{x\in\Omega}xf(x) = \frac{1}{6}\sum_{x = 1}^{6}x = \frac{1}{6} \cdot (1+2+3+4+5+6) = \frac{7}{2}=3.5 \\ \Var(X) &= \sum_{x \in \Omega}(x - \mu)^2f(x) = \frac{1}{6}\sum_{x = 1}^{6}\left(x - \frac{7}{2}\right)^2 \\ &=\frac{1}{6}\left(\left(-\frac{5}{2}\right)^2+\left(-\frac{3}{2}\right)^2+\left(-\frac{1}{2}\right)^2+\left(\frac{1}{2}\right)^2+\left(\frac{3}{2}\right)^2+\left(\frac{5}{2}\right)^2\right) = \frac{35}{12}=2.9167. \end{aligned}\end{split}\]

Tunnetuille jakaumille on laskettu valmiiksi kaavat odotusarvolle ja varianssille. Seuraavassa lauseessa annetaan aikaisemmin esillä olleiden diskreettien jakaumien odotusarvot ja varianssit. Todistus sivuutetaan.

Lause 3.1.4

Jos \(X \sim \mathrm{Tasd}(1, n)\), niin

\[\rE(X) = \frac{n + 1}{2} \qquad\text{ja}\qquad \Var(X) = \frac{n^2 - 1}{12}.\]

Jos \(X \sim \mathrm{Hyperg}(N,m,n)\), niin

\[\rE(X) = \frac{nm}{N} \qquad\text{ja}\qquad \Var(X) = \frac{nm(N-m)(N-n) }{N^3-N}.\]

Jos \(X \sim \mathrm{Geo}(p)\), niin

\[\rE(X) = \frac{1}{p} \qquad\text{ja}\qquad \Var(X) = \frac{1-p}{p^2}.\]

Jos \(X \sim \mathrm{Ber}(p)\), niin

\[\rE(X) = p \qquad\text{ja}\qquad \Var(X) = p(1-p).\]

Jatkuvat satunnaismuuttujat

Määritelmä 3.1.5

Jatkuvan satunnaismuuttujan \(X\), jonka otosavaruus on \(\Omega\) ja tiheysfunktio \(f(x)\), odotusarvo \(\rE(X)\), varianssi \(\Var(X)\) ja keskihajonta \(\rD(X)\) ovat

\[\begin{split}\begin{aligned} \rE(X) &= \mu = \int_{-\infty}^\infty xf(x)\,\rd x, \\ \Var(X) &= \sigma^2 = \int_{-\infty}^\infty(x-\mu)^2f(x)\,\rd x, \\ \rD(X) &= \sigma = \sqrt{\Var(X)}. \end{aligned}\end{split}\]
Mikä on \(\rE(X)\), kun tiheysfunktio \(f_X(x) = \frac{1}{2}\) välillä \([0, 2]\)?
Mikä on \(\Var(X)\), kun tiheysfunktio \(f_X(x) = \frac{1}{2}\) välillä \([0, 2]\)?

Jälleen määritelmä edellyttää, että asianmukaiset integraalit suppenevat. Muussa tapauksessa tunnuslukuja ei ole olemassa. Huomaa samankaltaisuus diskreetin ja jatkuvan muuttujan tunnuslukujen määritelmissä: jatkuvassa tapauksessa summaus yksinkertaisesti korvataan integroinnilla. Jatkuvan satunnaismuuttujan odotusarvoon ja varianssiin liittyy samankaltainen fysikaalinen tulkinta kuin diskreettiinkin tapaukseen.

Esimerkki 3.1.6

Olkoon \(X\) jatkuva satunnaismuuttuja, jonka tiheysfunktio

\[f(x)=2x, \qquad\text{kun } 0 < x < 1.\]

Tällöin

\[\begin{split}\begin{aligned} \rE(X) &= \int_{-\infty}^{\infty}xf(x)\,\rd x = \int_{0}^{1}2x^2\,\rd x = \sij{0}{1}\frac{2}{3}x^3 = \frac{2}{3}=0.667, \\ \Var(X) &= \int_{-\infty}^{\infty}(x - \mu)^2f(x)\,\rd x = \int_{0}^{1}2x\left(x - \frac{2}{3}\right)^2\,\rd x \\ &= \int_{0}^{1}\left(2x^3 - \frac{8}{3}x^2 + \frac{8}{9}x\right)\,\rd x = \sij{0}{1}\left(\frac{1}{2}x^4 - \frac{8}{9}x^3 + \frac{4}{9}x^2\right) = \frac{1}{18}=0.056. \end{aligned}\end{split}\]

Tällaisessa tilanteessa, missä jakauma ei ole mikään tunnettu jakauma, laskut Matlabilla ja R:ssä täytyy tehdä määrättyinä integraaleina. Matlabilla tulokset saadaan komennoilla

   syms x  % muodostetaan symbolinen muuttuja x|
   Ex = int(x*2*x, x, 0, 1)  % odotusarvo|
   Var = int((x-Ex)^2*2*x, x, 0, 1)  % varianssi

R:ssä laskut saadaan numeerisesti komennoilla

   xf <- function(x) {x*2*x}  # muodostetaan funktio x*f(x)
   Ex <- integrate(xf, 0, 1)  # odotusarvo muuttujaan Ex
   xxf <- function(x) {(x-Ex[[1]])^2*2*x }  # funktio (x-E(x))^2*f(x)
   Var <- integrate(xxf, 0, 1)  # odotusarvo muuttujaan Var

Muuttuja Ex voi olla lista, jossa 1. komponentti on odotusarvo ja 2. komponentti on tulokseen sisältyvän absoluuttisen virheen maksimi. Siksi varianssia laskettaessa käytetään valitaan listan ensimmäinen alkio muodossa Ex[[1]].

Kuitenkin tunnetujen jakaumien odotusarvoille ja variansseille on määritetty valmiita kaavoja. Aikaisemmin esillä olleiden jatkuvien jakaumien odotusarvot ja varianssit annetaan seuraavassa lauseessa. Myöhemmin uusien jakaumien yhteydessä annetaan aina myös odotusarvojen ja varianssien kaavat.

Lause 3.1.7

Jos \(X \sim \Tas(a, b)\), niin

\[\rE(X)=\frac{a+b}{2}\qquad\text{ja}\qquad\Var(X)=\frac{(b-a)^2}{12}.\]

Jos \(X \sim \Exp(\lambda)\), niin

\[\rE(X) = \frac{1}{\lambda} \qquad\text{ja}\qquad \Var(X) = \frac{1}{\lambda^2}.\]

Tarkastellaan kahta satunnaismuuttujaa \(S\) ja \(P\). Alla olevaan kuvaan on piirretty satunnaismuuttujien tiheysfunktiot, satunnaismuuttujan \(S\) tiheysfunktio sinisellä ja satunnaismuuttujan \(P\) punaisella. Päättele jakaumien muotojen perusteella vastaukset seuraaviin kysymyksiin.

../_images/odotusarvo-jakaumat.png
Kumman satunnaismuuttujan odotusarvo on suurempi?
Kumman satunnaismuuttujan keskihajonta on suurempi?
Kumman satunnaismuuttujan varianssi on suurempi?

Fraktiilit

Odotusarvo on yksi jakauman keskikohtaa kuvaava tunnusluku. Toinen yleisesti käytetty keskiluku on mediaani, joka on erikoistapaus ns. fraktiileista eli prosenttipisteistä.

Määritelmä 3.1.8

Satunnaismuuttujan \(X\) p-fraktiili eli 100p-prosenttipiste on luku \(x_p\),

jolle \(P(X\leq x_p)=p\)

0.5-fraktiilia eli 50-prosenttipistettä kutsutaan mediaaniksi (median) \(\mathrm{Md}(X)\).

Mediaanille \(P(X\leq Md(x))=0.5\).

0.25-fraktiili eli 25-prosenttipiste on nimeltään 1. kvartiili eli alakvartiili.

0.75-fraktiili 75-prosenttipiste on 3. kvartiili eli yläkvartiili.

10%:n välein olevia prosenttipisteitä kutsutaan desiileiksi.

Fraktiilit voidaan esittää myös kertymäfunktion \(F(x)=P(X<x)\) avulla. Mediaani toteuttaa ehdon \(F(Md(X))=0.5\). Mediaani jakaa jakauman kahteen todennäköisyydeltään yhtäsuureen osaan. Yleisesti p-fraktiili \(x_p\) on luku, jolle \(F(x_p)=p\).

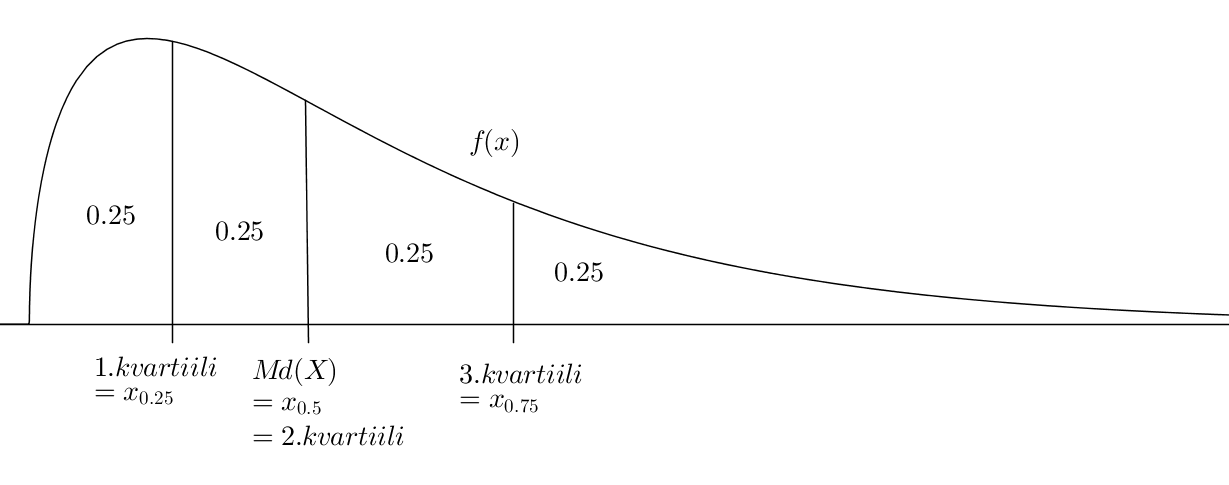
Kuvassa on esitetty, miten kvartiilit jakavat jakauman todennäköisyyden neljään yhtäsuureen osaan. 0. kvartiili on jakauman otosavaruuden alaraja, 2. kvartiili on sama kuin mediaani ja 4. kvartiili on otosavaruuden yläraja.

../_images/fraktiili.png

Diskreeteillä satunnaismuuttujilla kertymäfunktio on porrasfunktio ja ei välttämättä saa lainkaan arvoa \(p\) fraktiilia \(x_p\) laskettaessa. Fraktiiliksi valitaan se otosavaruuden pienin alkio \(x_i\), jolle kertymäfunktio on vähintään \(p\). Ts. edellisellä alkiolla \(F(x_{i-1})<p\), mutta \(F(x_i)\geq p\).

Fraktiilit saa ohjelmilla käyttämällä kertymäfunktion käänteisfunktiota. Yleisesti fraktiili \(x_p\) saadaan Matlabilla komennolla

   nimiinv(p,parametrit)

missä nimi on jakauman yksilöivä nimi, p on fraktiiliin liittyvä todennäköisyys ja parametrit ovat jakauman parametrit, yksi tai useampia.

R:ssä vastaava komento on

   qnimi(p,parametrit)

Esimerkki 3.1.9

Eksponenttijakaumaa noudattavan satunnaismuuttujan \(T\sim\mathrm{Exp}(\lambda)\) mediaani on

\[Md(T)=\dfrac{\ln(2)}{\lambda}\]

Tämän voi varmistaa laskemalla todennäköisyyden \(P\left(T\leq \dfrac{\ln(2)}{\lambda}\right)\) esimerkiksi integroimalla tiheysfunktion \(f(t)=\lambda e^{-\lambda t}\) välillä \([0, \frac{\ln(2)}{\lambda}]\) ja saa arvoksi \(\frac12\).

Esimerkiksi jos \(T\sim\mathrm{Exp}(2)\), niin mediaani on \(Md(T)=\dfrac{\ln(2)}{2}=0.3466\).

Matlabilla tämän saa komennolla

   expinv(0.5, 1/2)

Huomaa, että Matlabissa eksponenttijakauma on määritelty toisella tavalla ja siksi toiseksi parametriksi valitaan käänteisluku 1/2.

R:ssä sama mediaani lasketaan komennolla

   qexp(0.5, 2)

Esimerkki 3.1.10

Satunnaismuuttuja \(X\sim\mathrm{Geo}(0.2)\) noudattaa geometrista jakaumaa tiheysfunktiona \(f(x)=p(1-p)^{x-1}\) otosavaruudessa \(\Omega=\{1,2,3,\cdots\}\). Kun lasketaan kertymäfunktion arvoja, saadaan

\[\begin{split}\begin{array}{rcl} F(1)&=f(1)=0.2\cdot 0.8^0 = 0.2\\ F(2)&=F(1)+f(2)= 0.2+0.2\cdot 0.8^1= 0.36\\ F(3)&=F(2)+f(3)= 0.36+0.2\cdot 0.8^2= 0.488\\ F(4)&=F(3)+f(4)= 0.488+0.2\cdot 0.8^3= 0.5904 \end{array}\end{split}\]

Koska \(F(3)=0.488<0.5\) ja \(F(4)=0.5904 \geq 0.5\), on tämän geometrisen jakauman mediaani \(Md(X)=4\)

Matlabilla saadaan komennolla

   geoinv(0.5, 0.2)

mediaaniksi \(Md(X)=3\). Vastaus poikkeaa edellisestä siksi, että Matlabin käyttämä satunnaismuuttujan tulkinta on epäonnistumisten määrä ennen 1. onnistumista otosavaruutena \(\Omega=\{0,1,2,\cdots\}\). Tämän kurssimonisteen käyttämä tulkinta puolestaan on monennellako toistokerralla tulee 1. onnistuminen otosavaruutena \(\Omega=\{1,2,3,\cdots\}\).

R:ssä vastaava komento on ja mediaani \(Md(X)=3\) saadaan komennolla

   qgeom(0.5, 0.2)

Esimerkki 3.1.11

Odotusarvo ja mediaani ovat molemmat jakauman keskikohtaa luonnehtivia tunnuslukuja. Ne voivat poiketa toisistaan paljonkin. Vastaavat käsitteet tilastollisessa havaintoaineistossa ovat (otos)keskiarvo ja (otos)mediaani. Otoskeskiarvo on muuttujan arvojen summa jaettuna lukumäärällä ja otosmediaani on suuruusjärjestykseen laitettujen arvojen keskimmäinen arvo tai kahden keskimmäisen arvon keskiarvo, jos arvoja on parillinen määrä. Esimerkiksi aineistossa on yrityksen kaikkien työntekijöiden kuukausipalkat ja on saatu arvot 1500, 1600, 1700, 1800, 20000, joista yksi on selvästi muita suurempi. Nyt keskiarvo on 5320 ja mediaani on 1700. Tässä mediaani kuvaa paremmin keskimääräistä palkkatasoa.

Palautusta lähetetään...